Логарифмы! Очень срочно надо 6.39 и 6.41,нужно решение

Логарифмы! Очень срочно надо 6.39 и 6.41,нужно решение
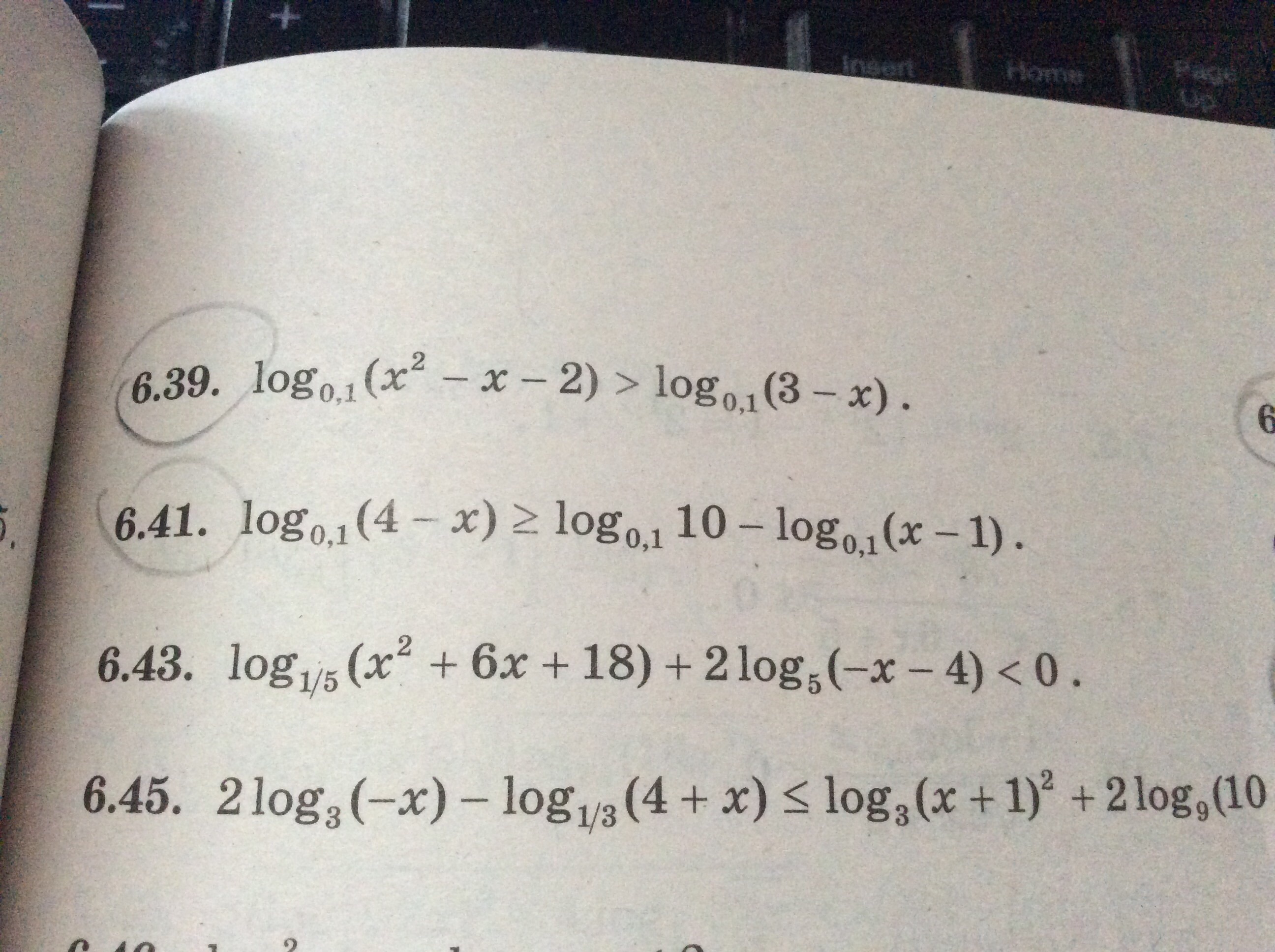
- Предмет:
  Математика
- Автор:
  roseokan
- 5 лет назад

Ответы 2

Спасибо огромное
- Автор:
  dustinxkqw
- 5 лет назад
- 0
$\log_{0,1}(x^2-x-2)\ \textgreater \ \log_{0,1}(3-x), \\ \left\{\begin{array}{c}x^2-x-2\ \textgreater \ 0,\\3-x\ \textgreater \ 0,\\x^2-x-2\ \textless \ 3-x,\end{array}ight. \ \left\{\begin{array}{c}(x+1)(x-2)\ \textgreater \ 0,\\x-3\ \textless \ 0,\\x^2-5\ \textless \ 0,\end{array}ight. \\ \left\{\begin{array}{c}(x+1)(x-2)\ \textgreater \ 0,\\x-3\ \textless \ 0,\\(x+\sqrt{5})(x-\sqrt{5})\ \textless \ 0,\end{array}ight. \ \left\{\begin{array}{c} \left [{{x\ \textless \ -1,} \atop {x\ \textgreater \ 2,}} ight.\\x\ \textless \ 3,\\-\sqrt{5}\ \textless \ x\ \textless \ \sqrt{5},\end{array}ight. \\ \left [ {{-\sqrt{5}\ \textless \ x\ \textless \ -1},} \atop {2\ \textless \ x\ \textless \ \sqrt{5};}} ight. \\ x\in(-\sqrt{5};-1)\cup(2;\sqrt{5}).$ $\log_{0,1}(4-x) \geq \log_{0,1}10-\log_{0,1}(x-1), \\ \log_{0,1}(4-x)+\log_{0,1}(x-1) \geq \log_{0,1}10, \\ \log_{0,1}(4-x)(x-1) \geq \log_{0,1}10, \\ \left\{\begin{array}{c}4-x\ \textgreater \ 0,\\x-1\ \textgreater \ 0,\\(4-x)(x-1) \leq 10;\end{array}ight. \ \left\{\begin{array}{c}x-4\ \textless \ 0,\\x-1\ \textgreater \ 0,\\x^2-5x+4 \geq 10;\end{array}ight. \ \left\{\begin{array}{c}x\ \textless \ 4,\\x\ \textgreater \ 1,\\x^2-5x-6 \geq 0;\end{array}ight.$ $\left\{\begin{array}{c}x\ \textless \ 4,\\x\ \textgreater \ 1,\\(x+1)(x-6)\geq 0;\end{array}ight. \ \left\{\begin{array}{c}1<x<4,\\ \left [ {{x \leq -1,} \atop {x \geq 6;}} ight.\end{array}ight. \\ x\in\varnothing.$
- Автор:
  bradyo9ki
- 5 лет назад
- 0
Добавить свой ответ