-
Тригонометрия, вообще не шарю
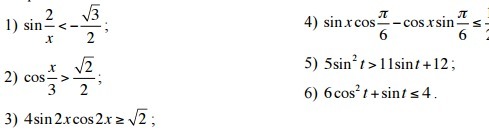
-
Предмет:
Математика -
Автор:
kitty95 - 5 лет назад
-
Ответы 1
-
1sin(2/x)<-√3/24π/3+2πn<2/x<5π/3+2πn2π/3+πn<1/x<5π/6+πn6/5π+1/πn<x<5/6π+1/πn,n∈z2cos(x/3)>√2/2-π/4+2πn<x/3<π/4+2πn-3π/4+6πn,x,3π/4+6πn,n∈z34sin2xcos2x≥√22sin4x≥√2sin4x≥⇒2/2π/4+2πn≤4x≤3π/4+2πnπ/16+πn/2≤x≤3π/16+πn/2,n∈z4sinxcosπ/6-cosxsinπ/6≤1/2sin(x-π/6)≤1/25π/6+2πn≤x-π/6≤13π/6+2πnπ+2πn≤x≤7π/3+2πn,n∈z55sin²t>11sint+12sint=a5a²-11a-12>0D=121+240=361a1=(11-19)/10=-0,8 U a2=(19+11)/10=3[sint<-0,8⇒π+arcsin0,8+2πn<t<2π-arcsin0,8+2πn,n∈z[sint>3 нет решения,т.к.|sint|≤166cos²t-sint≤46-6sin²t-sint≤4sint=a6a²+a-2≥0D=1+48=49a1=(-1-7)/12=-2/3 U a2=(-1+7)/12=1/2[sint≤-2/3⇒π+arcsin2/3+2πn≤t≤2π-arcsin2/3+2πn,n∈z[sint≥1/2⇒π/6+2πn≤x≤5π/6+2πn,n∈z
-
Автор:
raul133 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
найдите корень уравнения -3×(8+x)+6X=-3
-
Предмет:
Математика -
Автор:
phantomtr9o - 5 лет назад
-
Ответов:
2 -
Смотреть
-
- почему в клетке никогда не бывает высокой концентрации кислорода?
-
you have received a voice message from your friend asking you to go clothes shopping with him
-
Предмет:
Английский язык -
Автор:
aiyanaeib6 - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
О какой особенности дыхания говорил Борис Заходер в своем стихотворении "В больнице"?
-Больной, дышите!
Не дышите!
-Ах, милый доктор,
Не смешите!
Вы думаете,
Вам решать -
Дышать мне или не дышать?
How much to ban the user?
1 hour
1 day
100 years
