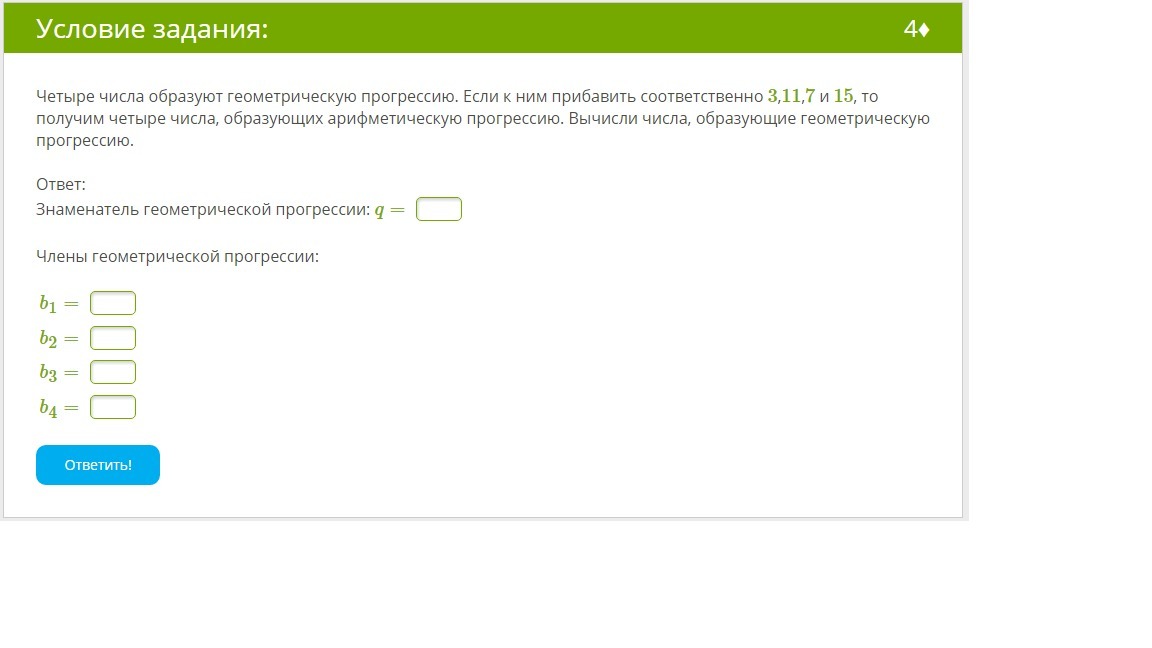
Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 3,11,7 и 15, то получим четыре числа, образующих арифметическую прогрессию. Вычисли числа, образующие геометрическую прогрессию.

4 числа образуют геом. прогрессию.b1; b2 = b1*q; b3 = b1*q^2; b4 = b1*q^3Если прибавить 3, 11, 7 и 15, получится ариф. прогрессияb1+3 = a1; b1*q+11 = a1+d; b1*q^2+7 = a1+2d; b1*q^3+15 = a1+3d.Получаем систему{ b1*q + 11 = b1 + 3 + d{ b1*q^2 + 7 = b1 + 3 + 2d{ b1*q^3 + 15 = b1 + 3 + 3dВыразим b1{ b1*(q - 1) = d - 8{ b1*(q^2 - 1) = 2d - 4{ b1*(q^3 - 1) = 3d - 12Разложим разности квадратов и кубов на скобки{ b1*(q - 1) = d - 8{ b1*(q - 1)(q + 1) = 2d - 4{ b1*(q - 1)(q^2 + q + 1) = 3d - 12Подставим 1 уравнение во 2 и 3 уравнения{ (d - 8)(q + 1) = 2d - 4{ (d - 8)(q^2 + q + 1) = 3d - 12Выразим q{ q + 1 = (2d - 4)/(d - 8) = (2d - 16 + 12)/(d - 8) = 2 + 12/(d - 8){ q^2 + q + 1 = (3d - 12)/(d - 8) = (3d - 24 + 12)/(d - 8) = 3 + 12/(d - 8)Вычитаем из 3 уравнения 2 уравнениеq^2 = 11) q1 = -1 q + 1 = 2 + 12/(d - 8) = 012/(d - 8) = -26 = -(d - 8) = 8 - dd = 2b1 = (d - 8)/(q - 1) = (2 - 8)/(-1 - 1) = (-6)/(-2) = 3Это числа 3, -3, 3, -3. Если прибавить 3,11,7,15, получится 6,8,10,12.2) q2 = 1q + 1 = d - 8 = 2d = 10b1 = (d - 8)/(q - 1) = (10 - 8)/(1 - 1) - не определено.