-
Помогите пожалуйста решить уравнения. Заранее огромное спасибо
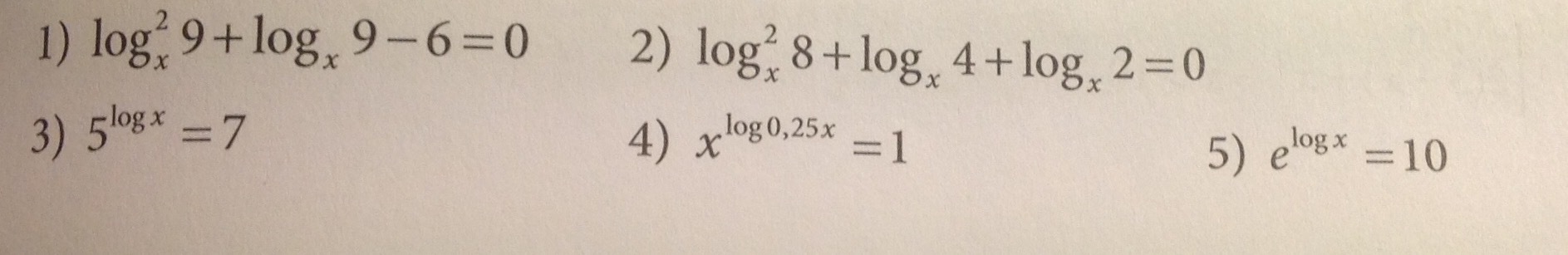
-
Предмет:
Математика -
Автор:
mayra - 5 лет назад
-
Ответы 1
-
Когда решаешь задачи с логарифмами, начинать надо с обл. опр.1) Обл.опр.: x > 0; x =/= 1 Замена log_x (9) = yy^2 + y - 6 = 0Обыкновенное квадратное уравнение.(y + 3)(y - 2) = 0y1 = log_x (9) = -3; x^(-3) = 9; x^3 = 1/9; x1 = 1/∛9y2 = log_x (9) = 2; x^2 = 9; x2 = 32) Обл.опр.: x > 0; x =/= 1log_x (8) = log_x (2^3) = 3*log_x (2); log^2_x (8) = 9log^2_x (2)log_x (4) = log_x (2^2) = 2log_x (2).Замена log_x (2) = y9y^2 + 2y + y = 9y^2 + 3y = 03y(3y + 1) = 0y1 = log_x (2) = 0; x^0 = 2; решений нетy2 = log_x (2) = -1/3; x^(-1/3) = 2; x^(1/3) = 1/2; x = 1/2^3 = 1/83) Что такое log x без основания логарифма? Это натуральный?В русскоязычной литературе натуральный логарифм обозначается ln.Обл.опр.: x > 05^(ln x) = 7По определению, логарифм - это показатель, в который надо возвести основание, чтобы получить результат. У нас в показателе написано ln x.log5 (7) = ln xx = e^(log5 (7))4) x^(ln (0,25x)) = 1Обл.опр.: x > 0; x =/= 1Любое число в 0 степени равно 1, поэтомуln (0,25x) = 0Логарифм 1 равен 00,25x = 1x = 45) e^(ln x) = 10По основному свойству логарифма a^(log_a (b)) = b, поэтомуe^(ln x) = x = 10x = 10
-
Автор:
friendokc0m - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Запишите четыре значения X ,чтобы неравенство было верным :0,08 <x <0,081
-
Предмет:
Математика -
Автор:
ashleer4u4 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
что? такое фонетика?пожалуйста
-
Предмет:
Русский язык -
Автор:
orion - 5 лет назад
-
Ответов:
4 -
Смотреть
-
-
помогите разгадать кроссворд:
1) the four parts of the year(7букв)
2)when the sun is shining(5 букв)
3)the cars, buses and trucks using a road(7 букв)
4)short periods of rain(7 букв)
5)wet weather with very strong winds(6 букв)
-
Предмет:
Английский язык -
Автор:
kerrydecker - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Составьте схему к предложению:
Снег ложится на поля, на кусты, на деревья.-
Предмет:
Русский язык -
Автор:
balduino - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
