Помогите пожалуйста решить уравнение , не понимаю какие преобразования нужно сделать.

Помогите пожалуйста решить уравнение , не понимаю какие преобразования нужно сделать.
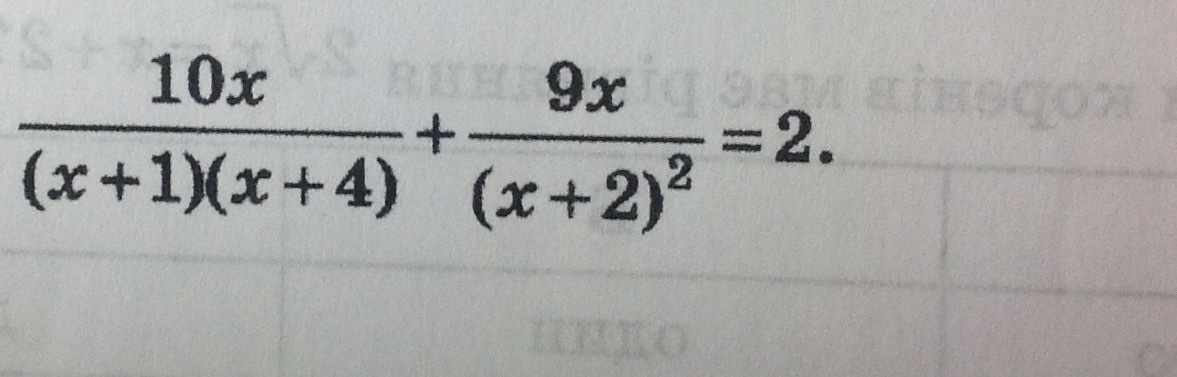
- Предмет:
  Математика
- Автор:
  copperdavidson
- 5 лет назад

Ответы 2

$\dfrac{10x}{(x+1)(x+4)} + \dfrac{9x}{(x+2)^2} =2$ ОДЗ: $\begin{cases} & \text{ } x+1 e 0 \\ & \text{ } x+4e 0 \\ & \text{ } x+2e 0 \end{cases}\Rightarrow\begin{cases} & \text{ } xe -1 \\ & \text{ } xe -4 \\ & \text{ } xe -2 \end{cases}$ Домножим обе части уравнения на $(x+1)(x+4)(x+2)^2$ $10x(x+2)^2+9x(x+1)(x+4)=2(x+2)^2(x+1)(x+4)\\ \\ 10x(x^2+4x+4)+9x(x^2+5x+4)-2(x^2+4x+4)(x^2+5x+4)=0$ Разделим обе части уравнения на $x^2$ , получаем: $10\bigg( x+\dfrac{4}{x}+4 \bigg)+9\bigg(x+ \dfrac{4}{x} +5\bigg)-2\bigg( x+\dfrac{4}{x}+4 \bigg)\bigg( x+\dfrac{4}{x}+5 \bigg)=0$ Пусть $\bigg( x+\dfrac{4}{x} \bigg)=t$ , тогда исходное уравнение будет иметь такое уравнение: $10(t+4)+9(t+5)-2(t+4)(t+5)=0\\ 10t+40+9t+45-2t^2-18t-40=0\\ 2t^2-t-45=0$ Вычислим дискриминант квадратного уравнения: $D=b^2-4ac=(-1)^2-4\cdot2\cdot(-45)=361$ Поскольку $D\ \textgreater \ 0$ , то квадратное уравнение имеет 2 корня. Найдем эти корни: $t_1= \dfrac{-b+ \sqrt{D} }{2a} = \dfrac{1+19}{2\cdot2} =5;\\ \\ \\t_2= \dfrac{-b- \sqrt{D} }{2a} = \dfrac{1-19}{2\cdot2} =- \dfrac{9}{2}$ Обратная замена: $x+ \dfrac{4}{x} =-\dfrac{9}{2} \,\,\,\, \bigg|\cdot 2x\\ \\ 2x^2+9x+8=0\\ D=b^2-4ac= 9^2-4\cdot2\cdot8=17$ Найдем корни по формулам: $x_1_,_2= \dfrac{-b\pm \sqrt{D}}{2a} = \dfrac{-9\pm \sqrt{17} }{4}$ $x+ \dfrac{4}{x} =5\,\,\, \bigg|\cdot x\\ \\ x^2-5x+4=0$ По т. Виета: $x_3=1;\,\,\,\,\,\,\, x_4=4.$ Ответ: $\dfrac{-9\pm \sqrt{17} }{4};1;4.$
- Автор:
  amir160
- 5 лет назад
- 0
Ответ ответ ответ ответ ответ ответ
- Автор:
  sydneefnkt
- 5 лет назад
- 0
Добавить свой ответ