Задать вопрос Регистрация
Помочь другим

  • Очередная 26 задача из ОГЭ.
    Две окружности, вписанные в угол О, касаются друг друга внешним образом.
    Точки A, B, C, D - точки касания окружностей и угла.
    O1 и O2 - центры окружностей.
    Их радиусы r = 15, R = 21.
    Рисунок прилагается.
    Требуется:
    1) Определить, параллельны ли отрезки AB и CD.
    (Мне кажется - не всегда!)
    2) Найти наименьшее расстояние между этими отрезками.
    Если они параллельны, то просто найти расстояние между ними.
    В учебнике ответ 35, но мне кажется, что это опечатка и должно быть 15+21=36.
    Как это решить?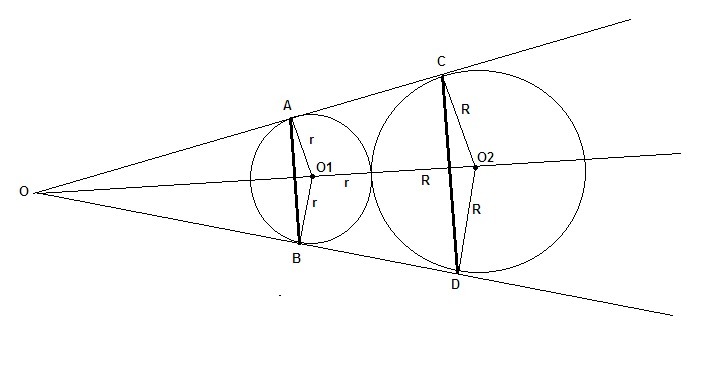

    question img

Ответы 3

  • это стандартная формула и свойство - угол О зависит только от R и r
  • Извините, я ничего не понял. Откуда вы взяли, что O2K = R-r и что угол O2O1K = a = половине угла О?

    • Автор:

      aránzazu
    • 5 лет назад
    • 0
  • отрезки AB и CD параллельны всегда - можно доказывать, рассматривая равенства всяких треугольников, но проще заметить, что имеется симметрия относительно биссектрисы угла О - если бы отрезки были не параллельны - не было бы симметрии.обозначим MN - расстояние между AB и CDдалее проще использовать тригонометриюобозначим половину угла О через  \alpha sin a= \frac{R-r}{R+r} \frac{r}{OB}=tg \alpha \\ OB= \frac{r}{tg \alpha } \\ \frac{OM}{OB}=cos \alpha \\ OM=OB*cos \alpha \frac{R}{OD}=tg \alpha \\ OD= \frac{R}{tg \alpha } \\ \frac{ON}{OD}=cos \alpha \\ ON=OD*cos \alpha OM=r* \frac{cos \alpha }{tg \alpha } = \frac{rcos^2 \alpha }{sin \alpha } \\ ON=R* \frac{cos \alpha }{tg \alpha } = \frac{Rcos^2 \alpha }{sin \alpha } OM=r* \frac{cos \alpha }{tg \alpha } = \frac{rcos^2 \alpha }{sin \alpha } \\ ON-OM=(R-r) \frac{cos^2 \alpha }{sin \alpha } =(R-r) \frac{1-sin^2 \alpha }{sin \alpha } ON-OM=(R-r) \frac{1- ( \frac{R-r}{R+r} )^{2} }{( \frac{R-r}{R+r} ) }= \frac{2r*2R}{R+r} = \frac{4rR}{R+r} ON-OM=\frac{4rR}{R+r}= \frac{4*15*21}{21+15} = \frac{1260}{36} =35 Ответ: 35

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years