-
ДАЮ 100 БАЛЛОВ! ДАТЬ ПОЛНОЕ РЕШЕНИЕ!
Мистер Фокс нарисовал параболу y=x2 и отметил на ней четыре точки K, L, M и N. Оказалось, что точки выбраны им так, что прямые KL и MN пересеклись на оси ординат. Чему равна абсцисса точки N, если абсциссы точек K, L и M соответственно равны 4, 3 и 5?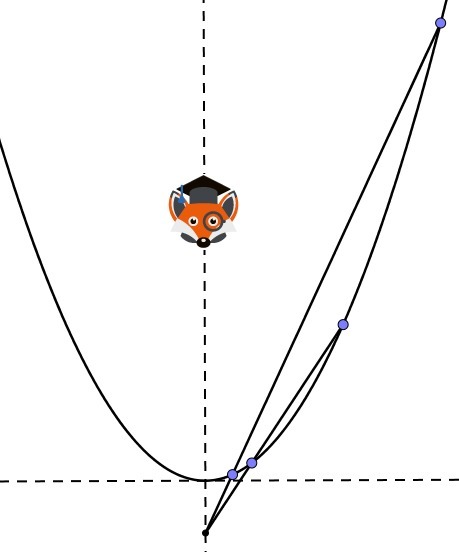
-
Предмет:
Математика -
Автор:
neveahzrd9 - 5 лет назад
-
Ответы 1
-
Мистер Фокс нарисовал параболу y=x2 и отметил на ней четыре точки K, L, M и N. Оказалось, что точки выбраны им так, что прямые KL и MN пересеклись на оси ординат. Чему равна абсцисса точки N, если абсциссы точек K, L и M соответственно равны 4, 3 и 5?
Определяем координаты точек на параболе у = х²: К(4; 16), L(3; 9), M(5, 25). Уравнение прямой KL: (х-4)/(3-4) = (у-16)/(9-16)
(х-4)/(-1) = (у-16)/( -7)
Сократим знаменатели на -1 и приведём к общему знаменателю: 7х-28 = у-16, 7х-у-12 = 0 или у = 7х-12. Эта прямая пересекает ось ординат в точке -12. Коэффициент наклона прямой MN равен (25+12)/5 = 37/5 = 7,4. Получаем уравнение прямой MN: y = 7,4x-12. Теперь находим точку N на параболе как точку пересечения параболы у=х² и прямой у=7,4х-12. х² = 7,4х-12. Получаем квадратное уравнение х²-7,4х+12 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-7.4)^2-4*1*12=54.76-4*12=54.76-48=6.76;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√6.76-(-7.4))/(2*1)=(2.6-(-7.4))/2=(2.6+7.4)/2=10/2=5 (это точка М),;
x₂=(-√6.76-(-7.4))/(2*1)=(-2.6-(-7.4))/2=(-2.6+7.4)/2=4.8/2=2.4.
Ответ: абсцисса точки N равна 2,4.
-
Автор:
demarcusmccullough - 5 лет назад
-
0
-
-
Добавить свой ответ
-
два поезда выехали с одной и той же станции одновременно в одном направлении один поезд двигался со скоростью 50 км в час а доугой 60 км .на каком расстоянии друг от друга окажутся поезда через 3 часа. На сколько часов один поезд прибудет раньше другого на станцию находящуюся на расстоянии 600 км от станции направления
-
Предмет:
Математика -
Автор:
birdyfisher - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Эссе на тему Наурыз аугыстым алық күні
на казахском языке
Пожалуйста срочна!!!
10 предложений
-
Предмет:
Қазақ тiлi -
Автор:
alvarez - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
просклоняйте попадежам местоимение ОНО МЫ ВЫ ОНИ
-
Предмет:
Русский язык -
Автор:
stevenpatterson - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
треугольник АВ=2см,АС=7см,ВС=6см СД=? S=?
-
Предмет:
Математика -
Автор:
nibbyqek4 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
