Найти площадь фигуры ограниченной линией p=3+cos(фи)

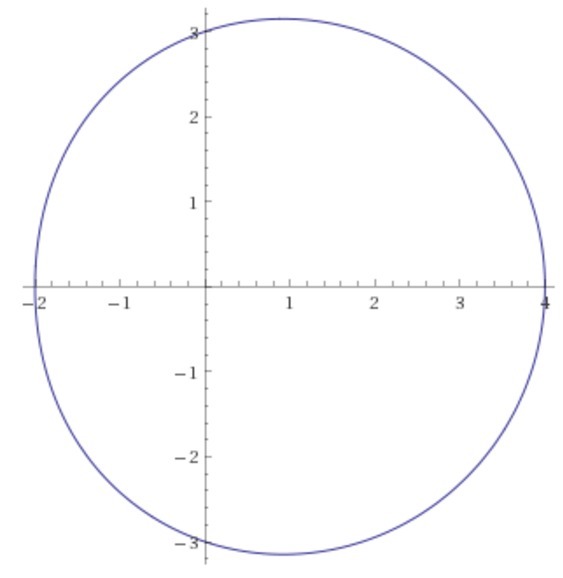
График во вложении. Площадь под кривой равна интегралу:\displaystyle S=\frac12\int_0^{2\pi}\rho^2(\varphi)\,d\varphi=\frac12\int_0^{2\pi}(9+6\cos\varphi+\cos^2\varphi)\,d\varphi=\frac{18\pi+\pi}2\\=\boxed{\frac{19\pi}2}(интеграл от 9 равен 9 * 2π, интеграл от косинуса по периоду равен 0, интеграл от (sin^2 phi + cos^2 phi) равен 2pi, а интеграл только от cos^2 phi равен половине от 2pi)Достаточно правдоподобный результат, учитывая, что фигура близка к окружности радиуса 3 с центром в точке (1, 0).