Задать вопрос Регистрация
Помочь другим

  • Что-то мозги тупят. Не могу решить. Надо найти предел.(по 2 замечательному пределу). За решение 60 баллов.

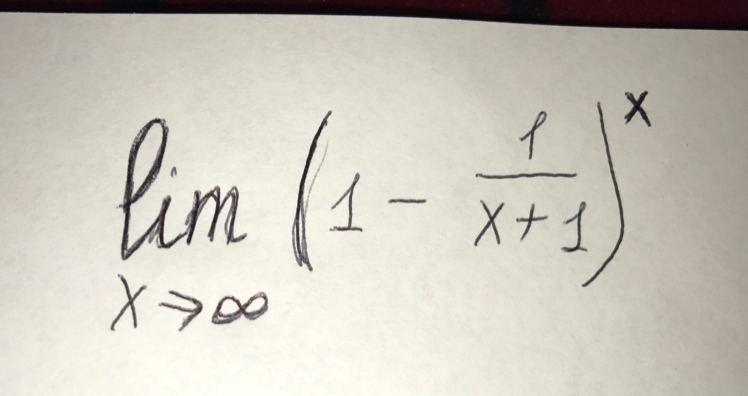
    question img

Ответы 5

  • Добавил фото

    • Автор:

      parker583
    • 5 лет назад
    • 0
  • Можете фото добавить ?

    • Автор:

      luke916
    • 5 лет назад
    • 0
  • Решения

    • Автор:

      panda14
    • 5 лет назад
    • 0
  • Воспользуемся вторым замечательным пределом:  \displaystyle \lim_{x \to \infty} \bigg(1+ \frac{1}{x} \bigg)^x=e\displaystyle \lim_{x \to \infty} \bigg(1+ \frac{-1}{x+1} \bigg)^\big{ x\cdot \frac{-1}{x+1}\cdot \frac{x+1}{-1} }=e^\big{ \lim_{x \to \infty} - \frac{x}{x+1} }=e^{-1}= \frac{1}{e}
    answer img
  • \displaystyle \bigger \lim_{x \to \infty} (1+\frac{1}{x})^x=e - Второй замечательный предел\displaystyle \bigger \lim_{x \to \infty} (1-\frac{1}{x+1})^x=1^{\infty}Неопределенность рода "единица в степени бесконечность"\displaystyle \bigger \lim_{x \to \infty} (1-\frac{1}{x+1})^x=\lim_{x \to \infty} (1+\frac{1}{-(x+1)})^x=\\\\=\lim_{x \to \infty} [(1+\frac{1}{-(x+1)})^{-(x+1)}]^{-\frac{1}{x+1}*x}=e^{\lim_{x \to \infty}-\frac{x}{x+1}}=\\\\=e^{\lim_{x \to \infty}-\frac{1}{1+\frac{1}{x}}}=e^{-1}=\frac{1}{e}}
    answer img

    • Автор:

      jack44
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years