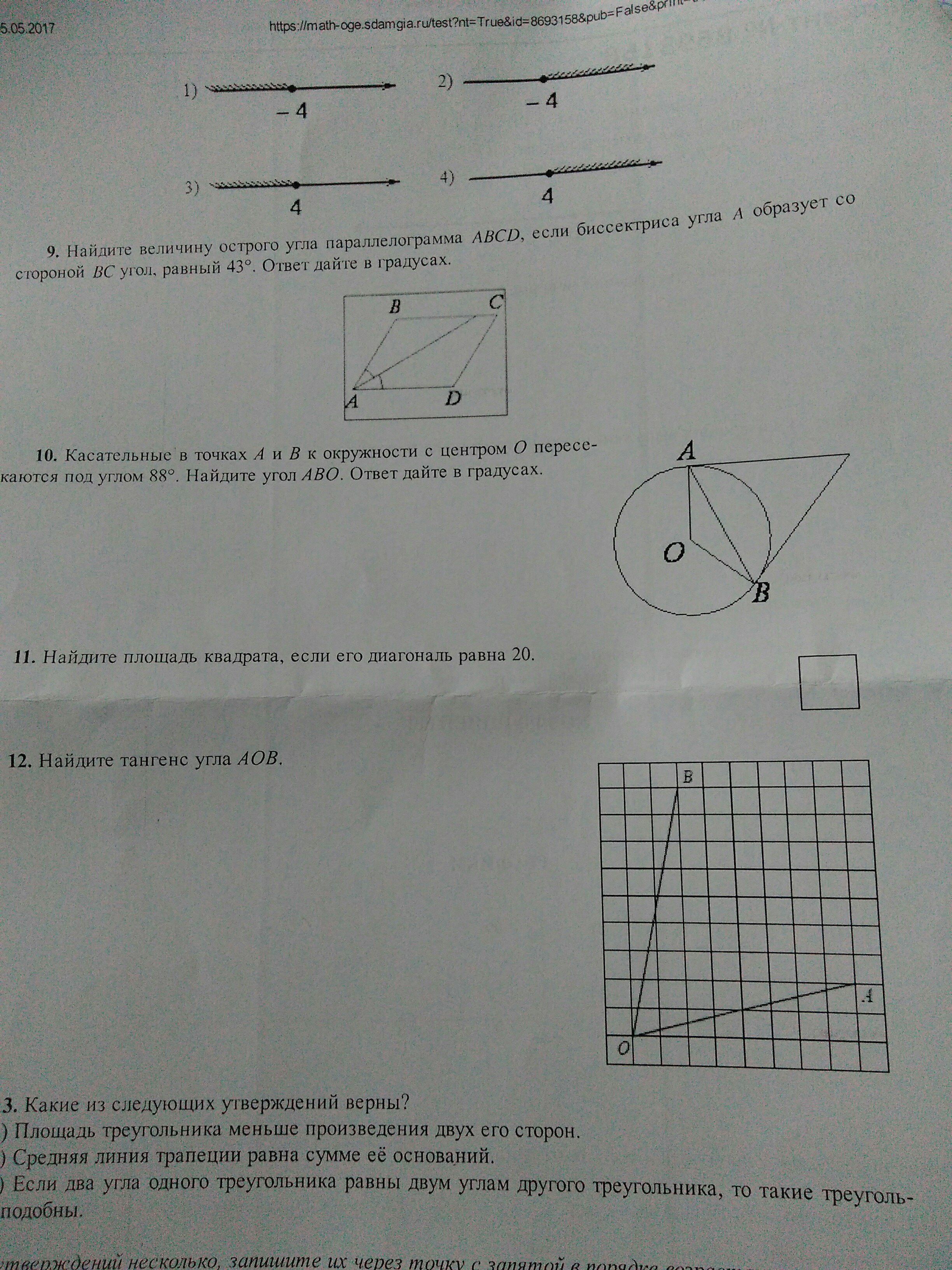
Помогите пожалуйста решить с 9 по 12 номер,с подробным объяснением. Очень нужно,заранее спасибо большое.)

9. Пусть точка пересечения биссектрисы угла A со стороной BC будет M.    ∠BMA=∠MAD=43°, так как BC║AD.     Тогда ∠BAD=∠BAM+∠MAD=86°.10. Пусть точка пересечения касательных M. Проведем отрезок MO, точка пересечения AB и OM будет K. ∠MOB=∠MBO-∠OMB=90°-∠AOB=90°-44°=46°. ∠ABO=∠KBO=∠OKB-∠KOB=90°-∠MOB=90°-46°=44°.11. Пусть сторона квадрата a. Площадь квадрата S=По теореме Пифагора ⇒⇒. Тогда S=200.12. Пусть проекция точки A на горизонтальную прямую М, а проекция точки В на вертикальную прямую К. Тогда ∠ВОА=∠КОМ-∠ВОК-∠АОМ;∠КОМ=90°, ∠ВОК=arctg, АОМ=arctg; Тогда tg(∠АОВ)=tg(90°-arctg-arctg).