Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста, нужно найти длину дуги кривой, заданной в декартовых координатах. Попадается такой интеграл, который не могу решить. Буду благодарен за помощь

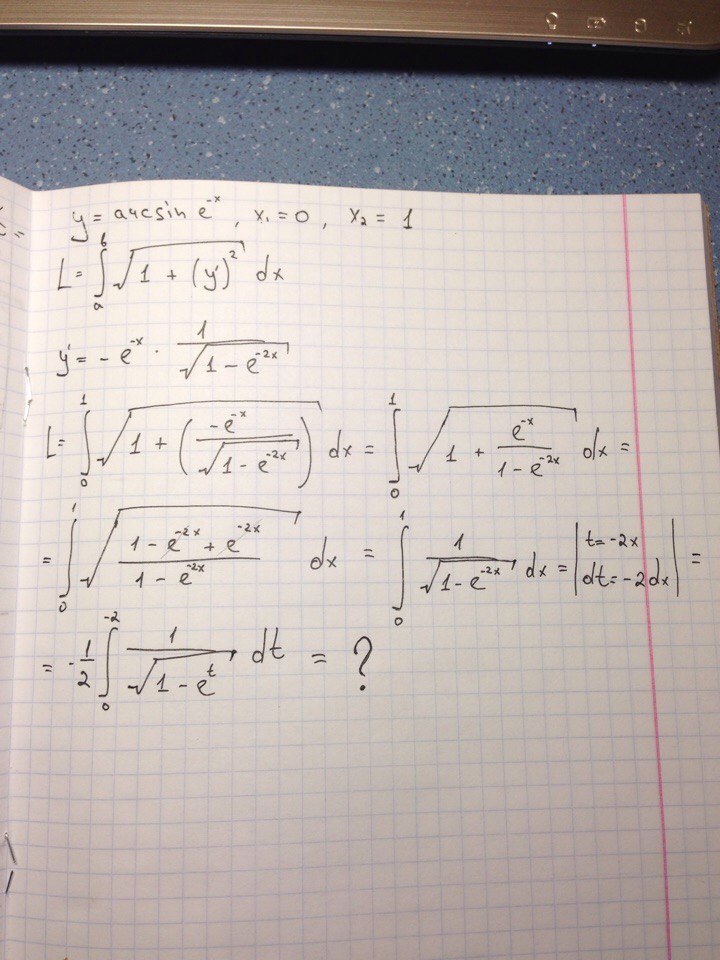
    question img

Ответы 2

  • Да, численный ответ с маткада и ваше решение сходится, спасибо вам огромнейшее!!!))

    • Автор:

      romeojqzl
    • 5 лет назад
    • 0
  • Посмотрите такой вариант, если верный, то обратную замену на Х и, собственно, вычисление, выполните сами :-)Перед заменой переменной интеграл можно было переписать немного по-другому, а именно: \int\limits^1_0 { \frac{1}{ \sqrt{1- e^{-2x} } } } \, dx = \int\limits^1_0 { \frac{1}{ \sqrt{1- \frac{1}{ e^{2x} } } } } \, dx = \int\limits^1_0 { \frac{ e^{x} }{ \sqrt{ e^{2x} -1} } } \, dx = \left[\begin{array}{ccc} e^{x} =t; \\dx= \frac{dt}{ e^{x} } = \frac{dt}{t} \\\end{array}ight] После замены еˣ=t; eˣdx=dt -> dx=dt/eˣ=dt/t получим интеграл: \int\limits^1_0 { \frac{1}{ \sqrt{ t^{2} -1} } } \, dt = ln|t+ \sqrt{ t^{2} -1} |

    • Автор:

      rios
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years