Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста решить дробь, заранее спасибо, прикреплена фотография , в которой дробь.

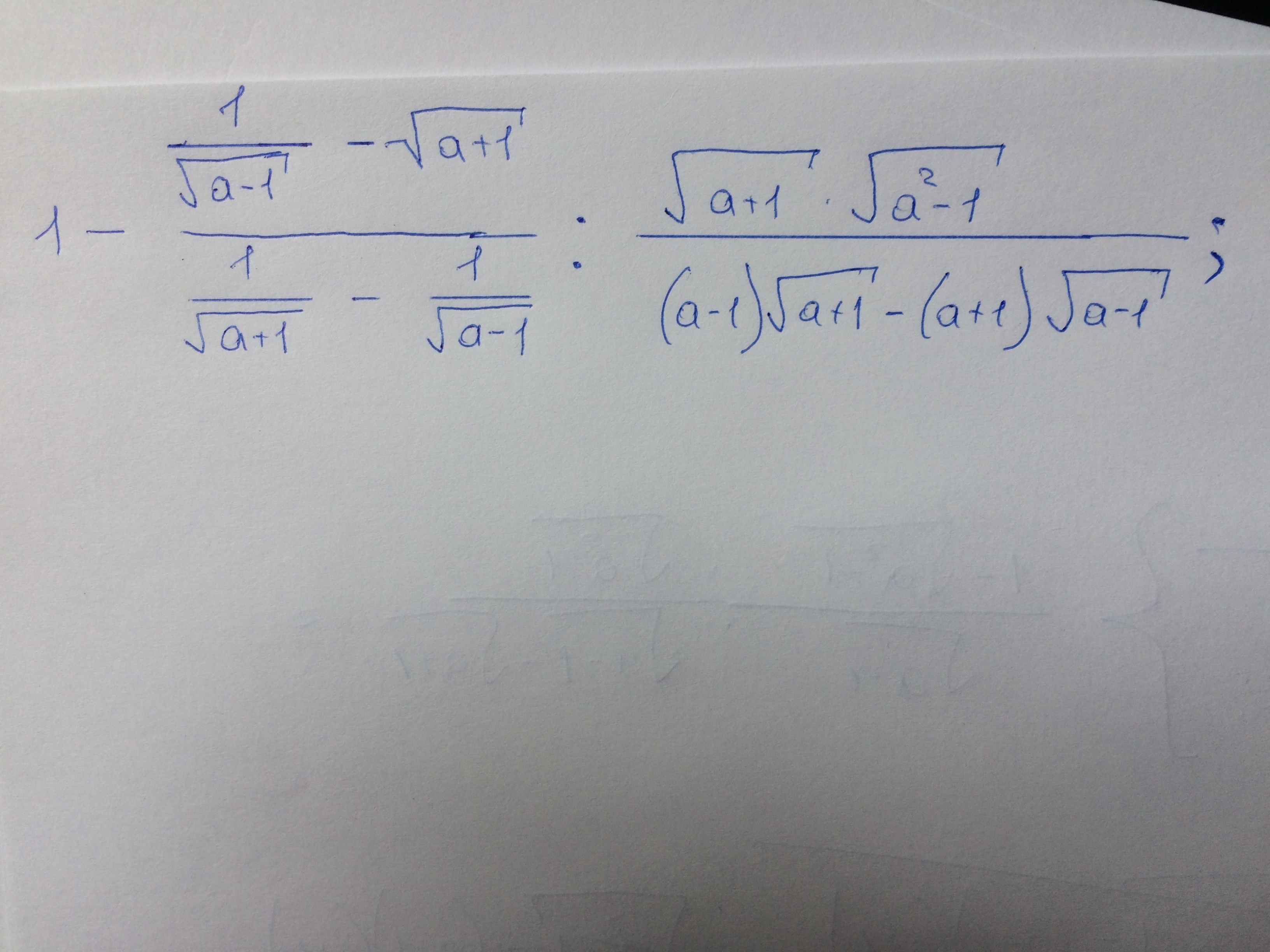
    question img

Ответы 1

  • Разберем по порядку.1) Первая дробь( \frac{1}{ \sqrt{a-1} }- \sqrt{a+1} ) : (\frac{1}{ \sqrt{a+1} }-\frac{1}{ \sqrt{a-1} })= \frac{1- \sqrt{(a+1)(a-1)} }{ \sqrt{a-1}}: \frac{ \sqrt{a-1} - \sqrt{a+1} }{ \sqrt{(a+1)(a-1)} } ==\frac{1- \sqrt{(a+1)(a-1)} }{ \sqrt{a-1}}* \frac{\sqrt{(a+1)(a-1)}}{ \sqrt{a-1} - \sqrt{a+1}} =\frac{1- \sqrt{(a+1)(a-1)} }{1}* \frac{\sqrt{(a+1)}}{ \sqrt{a-1} - \sqrt{a+1}} ==\frac{\sqrt{a+1}- (a+1)\sqrt{a-1} }{ \sqrt{a-1} - \sqrt{a+1}}2) Вторая дробь \frac{\sqrt{a+1}*\sqrt{a^2-1}}{(a-1)\sqrt{a+1}-(a+1)\sqrt{a-1}}= \frac{\sqrt{a+1}*\sqrt{(a-1)(a+1)}}{\sqrt{(a-1)(a+1)}*(\sqrt{a-1}-\sqrt{a+1})}= \frac{\sqrt{a+1}}{\sqrt{a-1}-\sqrt{a+1}} 3) Подставляем1-\frac{\sqrt{a+1}- (a+1)\sqrt{a-1} }{ \sqrt{a-1} - \sqrt{a+1}}:\frac{\sqrt{a+1}}{\sqrt{a-1}-\sqrt{a+1}}=1-\frac{\sqrt{a+1}- (a+1)\sqrt{a-1} }{ \sqrt{a-1} - \sqrt{a+1}}* \frac{\sqrt{a-1}-\sqrt{a+1}}{\sqrt{a+1}} =1-\frac{\sqrt{a+1}- (a+1)\sqrt{a-1} }{ \sqrt{a+1}}=1-(1-\sqrt{(a+1)(a-1)})=\sqrt{a^2-1}

    • Автор:

      yadira
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years