-
(2x+1)(x+4)-3x(x+2)<0 и
(5x+2)(x-1)-(2x+1)(2x-1)<27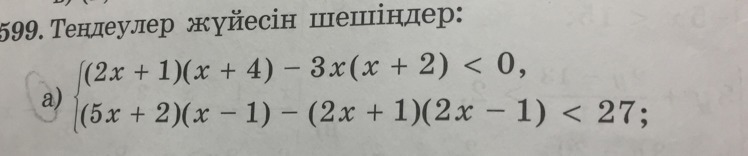
-
Предмет:
Математика -
Автор:
artemiorivera - 5 лет назад
-
Ответы 1
-
Преобразуем выражения:(2х+1)(х+4)-3х(х+2) < 0 2х²+8х+х+4-3х²-6х < 0-х²+3х+4 < 0х²-3х-4 > 0Второе:(5х+2)(х-1)-(2х+1)(2х-1) < 27 5х²-5х+2х-2-4х²-2х+2х+1 - 27 < 0х²-3х-28 < 0Получили систему:х²-3х-4 > 0х²-3х-28 < 0Берём каждую по отдельности и решаем:х²-3х-4 > 0х²-3х-4 = 0D = 9+16 = 25x1 = (3+5)/2 = 4x2 = (3-5)/2 = -1Рассмотрим три интервала (-∞; -1), (-1;4) и (4;+∞)На х є (-∞; -1) х²-3х-4 > 0На х є (-1; 4) х²-3х-4 < 0На х є (4;+∞) х²-3х-4 > 0Ответ первого неравенства х є (-∞; -1)\/(4;+∞)Переходим ко второму:х²-3х-28 < 0х²-3х-28 = 0D = 9 + 112 = 121x1 = (3+11)/2 = 7x2 = (3-11)/2 = -4Рассмотрим три интервала (-∞; -4), (-4;7) и (7;+∞)На х є (-∞; -4) х²-3х-28 > 0На х є (-4; 7) х²-3х-28 < 0На х є (7;+∞) х²-3х-28 > 0Ответ второго неравенства х є (-4;7)Ответом системы является наложение ответов первого и второго неравенства:общий ответ между х є (-∞; -1)\/(4;+∞) и х є (-4;7) это:х є (-4;-1)\/(4;7)Ответ: х є (-4;-1)\/(4;7)
-
Автор:
titovacd - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Что было в 1382году СРОЧНО!! (Не кратко)
-
Предмет:
История -
Автор:
ameliemlvr - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Взрывчатые вещества, которые применяются в быту?
-
Предмет:
Химия -
Автор:
alexzander - 5 лет назад
-
Ответов:
2 -
Смотреть
-
- характеристика природных ресурсов Северной Америки
-
Решите неравенство:
Ι2х+5Ι <х+4
How much to ban the user?
1 hour
1 day
100 years
