-
Необходимо полное решение! 40 балов хорошая цена
Приложение с пояснением!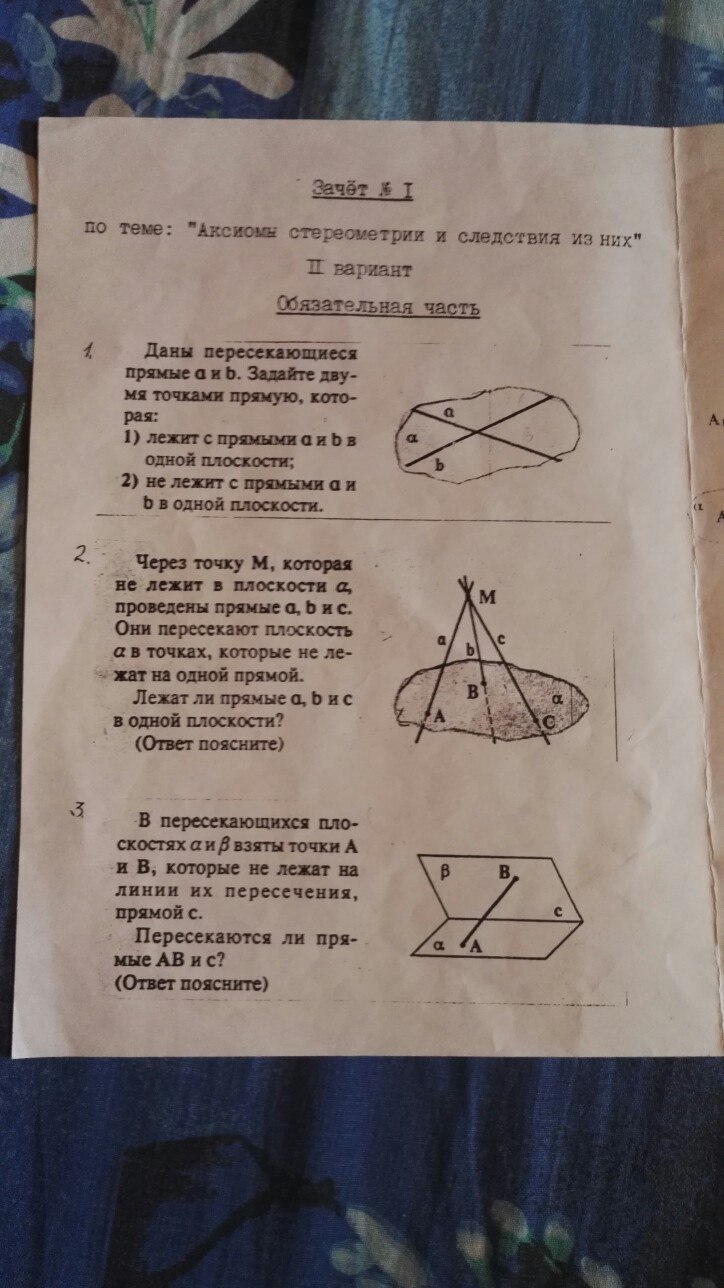
-
Предмет:
Математика -
Автор:
skunk - 6 лет назад
-
Ответы 1
-
1. a) Возьмем точки A и B такие, что:
Тогда прямая AB по соотв. аксиоме будет лежать в плоскости
б) Аналогично, возьмем, к примеру, такие точки:
Значит CD не будет лежать в плоскости
2. Рассмотрим плоскость
отличную от
Очевидно, что прямые
и
лежат в этой плоскости, т.к. у каждой из них имеются две точки, лежащие в ней. Теперь рассмотрим точку C.По условию, прямые пересекаются в точках, не лежащих на одной прямой, т.е.
. В то же время
Мы нашли точку прямой
(или MC), которая не принадлежит плоскости ABM, в которой лежат две другие прямые.Исходя из соотв. аксиомы
,
и
не могут лежать в одной плоскости.3. Нет, т.к. прямые являются скрещивающимися. Одна из прямых лежит в плоскости, вторая пересекает ее в точке, не лежащей на первой прямой.
-
Автор:
ajaxtaylor - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
За неделю в магазине продали 696 кг яблок, а бананов в 4 раза меньше . Сколько кг фруктов продали за неделю?
-
Предмет:
Математика -
Автор:
macynd6w - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
Название книги на тему:Человек защитник природы! ПРОШУ ПОМОГИТЕ НАПИШИТЕ НАЗВАНИЕ КНИГ КОТОРЫЕ ВЫ ЗНАИТЕ НА ЭТУ ТЕМУ
-
Предмет:
Окружающий мир -
Автор:
peter54 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
1)В средней полосе России, зимой большинство животных впадает в спячку или состояния анабиоза. Как вы можете объяснить такое поведение животных. Считаете ли вы его выгодным и почему?
2)Перед строителями встал вопрос выбора места для нового водохранилища. Как считаете вы, где его лучше построить в горах или на равнине. Почему?-
Предмет:
География -
Автор:
maritzadavenport - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Скласти речення з словом лишень ,лише, ото, ані. Пожалуйста помогите!!!
-
Предмет:
Українська мова -
Автор:
nevaeh - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
