Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста решить, даю 30 баллов.
    Показать, что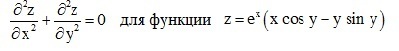

    question img

Ответы 2

  • Спасибо огромное!
  • z=e^{x}(x\, cosy-y\, siny)\\\\ \frac{\partial z}{\partial x} =e^{x}(x\, cosy-y\, siny)+e^{x}\, cosy=e^{x}(x\, cosy-y\, siny+cosy)\\\\ \frac{\partial ^2z}{\partial x^2}= e^{x}(x\, cosy-y\, sinu+cosy)+e^{x}\, cosy=\\\\=e^{x}(x\, cosy-y\, siny+2cosy)\\\\ \frac{\partial z}{\partial y} =e^{x}(-x\, siny-siny-y\, cosy)\\\\ \frac{\partial ^2z}{\partial y^2} =e^{x}(-x\, cosy-cosy-cosy+y\, siny)=\\\\=-e^{x}(x\, cosy-y\, sinx+2cosy)\\\\ \frac{\partial ^2z}{\partial x^2} + \frac{\partial ^2z}{\partial y^2} =0

    • Автор:

      carsen
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years