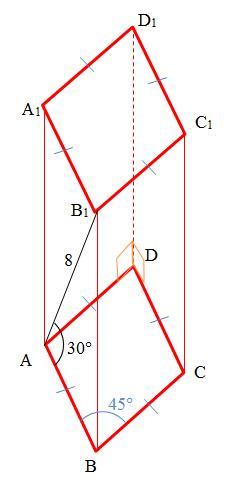
Основою прямої призми є ромб із гострим кутом 45°. Діагональ бічної грані дорівнює 8 см і утворює з площиною основи кут 30°. Знайдіть об'єм призми.

Ответ:

96√2 см³

Пошаговое объяснение:

Перевод: Основой прямой призмы является ромб с острым углом 45°. Диагональ боковой грани равна 8 см и образует с плоскостью основания угол 30°. Найдите объем призмы.

Решение. Прямая призма — это призма, у которой боковые рёбра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками.

Объём призмы равен произведению её высоты на площадь основания:

V=S•H, где S - площадь основания, H - высота призмы.

Сначала определим (см. рисунок) высоту призмы, то есть длину ребра BB₁. Так как треугольник ABB₁ прямоугольный, то по определению синуса угла:

sin∠BAB₁=sin30°=BB₁/AB₁, откуда H=BB₁=AB1·sin30°=8/2=4 см.

Далее, определению косинуса угла:

cos30°=AB/AB₁, откуда AB=AB₁⋅cos30°=8·√3/2=4√3 см.

Площадь ромба через сторону а и угол α определяется по формуле:

S=a²⋅sinα.

Тогда

V =a²⋅sinα⋅H=(4√3)²⋅sin45°·4=48⋅√2/2·4=96√2 см³.