Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.

Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.
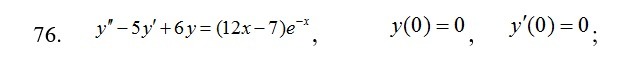
- Предмет:
  Математика
- Автор:
  jazmiegft6
- 6 лет назад

Ответы 1

Найдем сначала однородное уравнение: $y''-5y'+6y=0$ Пользуясь методом Эйлера, имеем характеристическое уравнение вида: $k^2-5k+6=0$ Корни которого $k_1=3$ и $k_2=2$ Общее решение однородного уравнения: $y_o=C_1e^{3x}+C_2e^{2x}$ 2) Найдем частное решениеПоложим $f(x)=(12x-7)e^{-x}$ $\alpha =-1;\,\,\,\, P_n(x)=12x-7),\,\,\, n=1$ тогда частное решение будем искать в виде: $\widetilde{y}=(Ax+B)e^{-x}$ Найдем первую и вторую производную $y'=-e^{-x}(Ax+B)+Ae^{-x}\\ \\ y''=e^{-x}(Ax+B)-Ae^{-x}-Ae^{-x}=e^{-x}(Ax+B)-2Ae^{-x}$ Подставим в исходное уравнение $Ax+B-2A-5(-(Ax+B)+A)+6(Ax+B)=12x-7\\ Ax+B-2A+5Ax+5B-5A+6Ax+6B=12x-7\\ 12Ax+12B-7A=12x-7$ Приравниваем коэффициенты при степени x $\displaystyle \left \{ {{12A=12} \atop {12B-7A=-7}} ight. \to \left \{ {{A=1} \atop {B=0}} ight.$ Тогда частное решение имеет вид: $\widetilde{y}=xe^{-x}$ Общее решение неоднородного уравнения: $y=y_o+\widetilde{y}=C_1e^{3x}+C_2e^{2x}+xe^{-x}$ $y'=3C_1e^{3x}+2C_2e^{2x}+e^{-x}-xe^{-x}$ Найдем решение задачи Коши $\displaystyle \left \{ {{C_1+C_2=0} \atop {3C_1+2C_2+1=0}} ight. \to \left \{ {{C_1=-1} \atop {C_2=1}} ight.$ $\boxed{y=-e^{3x}+e^{2x}+xe^{-x}}$
- Автор:
  jordan1odt
- 6 лет назад
- 0
Добавить свой ответ