Задать вопрос Регистрация
Помочь другим

  • Помогите по братски
    Пользуясь формулой Ньютона-Лейбница, вычислить определенный интеграл.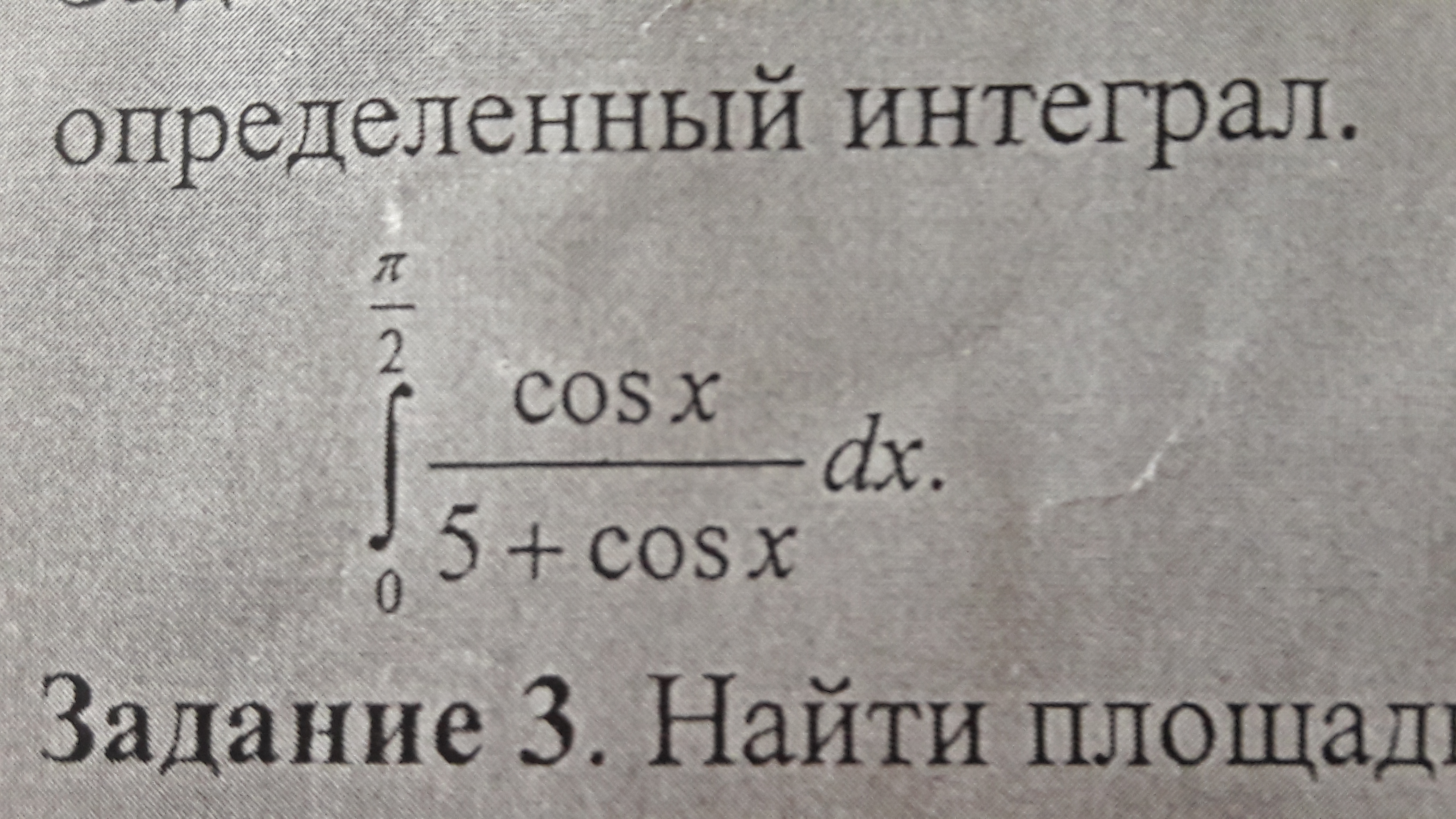

    question img

Ответы 1

  • \int \frac{(Cosx+5-5)dx}{5+Cosx} =\int(1- \frac{5}{5+Cosx} ) \, dx=| tg \frac{x}{2}=t \ x=2arctgt \ dx= \frac{2dt}{1+t^2} \\ Cosx= \frac{1-tg^2x}{1+tg^2x} = \frac{1-t^2}{1+t^2} |= \int dx-5\int \frac{ \frac{2dt}{1+t^2} }{5+\frac{1-t^2}{1+t^2}} =x-5 \int \frac{ \frac{2dt}{1+t^2} }{\frac{5+5t^2+1-t^2}{1+t^2}} = \\ = x-5 \int \frac{2dt}{6+4t^2} =x-5 \int \frac{2dt}{2(3+2t^2)} =x-5 \int \frac{dt}{3+2t^2} =x- \frac{5}{2} \int \frac{dt}{ \frac{3}{2} +t^2} = \\ = x- \frac{5}{2} \sqrt{\frac{ 2 }{ 3}}arctg \frac{t}{ \sqrt{\frac{ 3 }{ 2}}} +C=x- \frac{5}{ \sqrt{6} } arctg (\sqrt{ \frac{2}{3} } tg \frac{x}{2} )+C

    • Автор:

      heiditpua
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years