-
Найти неопределенные интегралы.
Решите кто сможет, для экзамена надо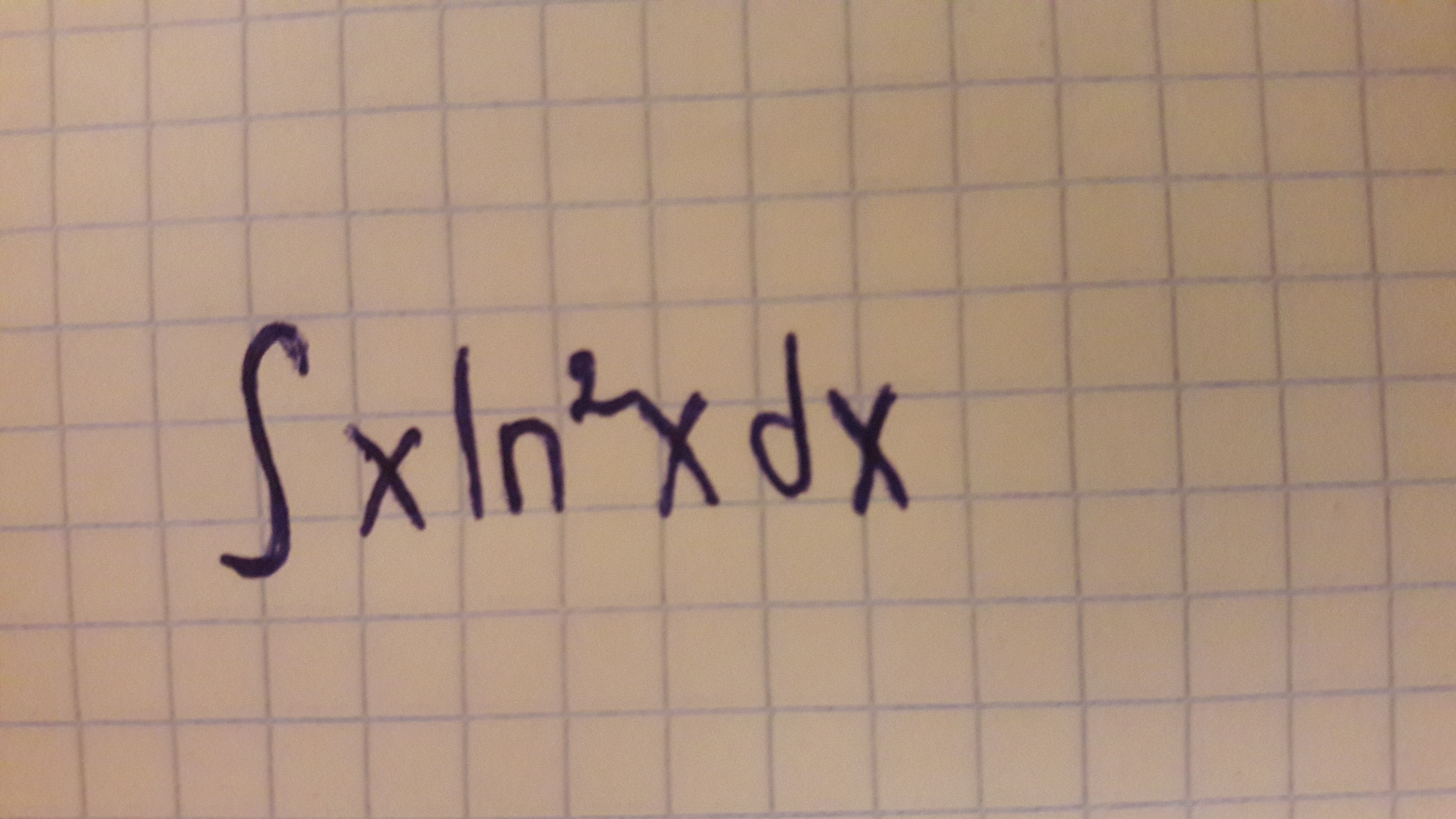
-
Предмет:
Математика -
Автор:
dereon - 6 лет назад
-
Ответы 3
-
В квадратных скобках необязательная часть - пояснения.
-
Автор:
chewbacca5uau - 6 лет назад
-
0
-
-
Спасибо
-
Автор:
djsjew - 6 лет назад
-
0
-
-
Рассмотрите такое решение:интеграл берётся методом интегрирования по частям: за dv обозначается хdx, за u - ln²x.
Для получившегося интеграла применяем правило ещё раз, только за u обозначаем lnx:
При желании ответ можно "упростить", подведя все дроби под общий знаменатель (4).
-
Автор:
peyton44 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
3х=6
решите пожалуйста-
Предмет:
Алгебра -
Автор:
pocketsbentley - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Задай вопросы к подчеркнутым словам( под. Слова будуь написаны капсом)
1.They are FILMS
2.They watch films ON SUNDAY
3.They watch FILMS on Sunday
4. They watch films AT SCHOOL
5. She is IN THE PARK
6.She runs IN THE EVENING
7. She runs IN THE PARK
8. She lives IN ITALY
9. They sing songs AT SCHOOL
10. They sing songs IN THE AFTERNOON-
Предмет:
Английский язык -
Автор:
rigobertofrye - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
37x+28x-3+4=2x+50x+3*20*654+4x+5
-
Предмет:
Математика -
Автор:
celloat3i - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
MY FRIEND
I have many friends. Most of them are my former
classmates but my best friend is Peter. He is fifteen.
Now he is a student of a college. He is a good student
because he studies hard and is very diligent. He wants
to become a good specialist and he is especially interested
in computers. He often helps me with my English lessons
and I'm grateful to him for that.
Now I want to tell you about his appearance. He is
rather tall and strong. He has an oval face, straight
nose, dark-brown hair, blue eyes and a nice smile. People
find him good-looking.
Peter goes in for sports. He plays football and basketball
well. Hi s basketball team is very popular at the
college.
We made friends with Peter when he and his family
moved to our house. We have very much in common:
we like the same music, we both like reading. In general my friend is a very interesting person: he is intelligent
and well-read.
But the most important thing is that Peter is honest
and kind. I can fully rely on him and trust everything
to him. Peter has a great sense of humour and I like to
spend my free time with him.
I have another friend. Her name is Natasha. She is a
schoolgirl and she lives next door. I like her very much.
She is a blonde with blue eyes, she is slim and pretty.
Her hair is long and she has a nice complexion. I like
all my friends very much. I think they are all my faithful
friends.
Переведите текст автор Агабекян-
Предмет:
Английский язык -
Автор:
micahkyrl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
