Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста!
    [tex] \sqrt{2}-2 \sqrt{2}sin^{2} \frac{15pi}{8} =[/tex]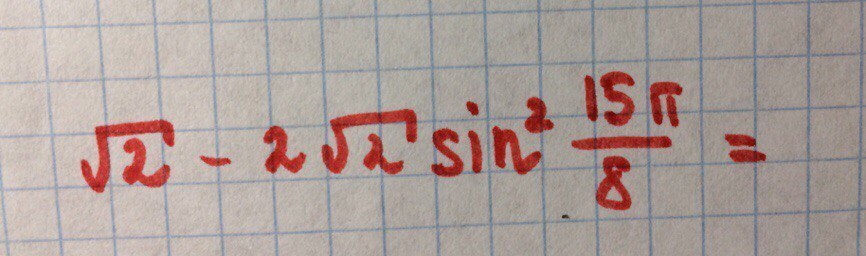

    question img

Ответы 2

  •    √2 - 2√2 * sin(15pi/8)*sin(15pi/8) =    √2 - 2√2 * ( - sin(pi/8))*( - sin(pi/8)) = = √2 - 2√2 * ( (1/2*√(2 - √2))^2) = = √2 - 2√2 * ( 1/4* (2 - √2)) = = √2 + 1 - √2 = 1Ответ1P.S. Таблица значений тригонометрических функций нестандартных углов
    answer img
  • \sqrt{2} -2 \sqrt{2}* sin^2 \frac{15 \pi }{8} =\sqrt{2} -2 \sqrt{2} *sin^2(2 \pi - \frac{ \pi }{8} )==\sqrt{2} -2 \sqrt{2} *sin^2 \frac{ \pi }{8} =\sqrt{2} -2 \sqrt{2} * \frac{1-cos \frac{ \pi }{4} }{2} =\sqrt{2} - \sqrt{2} * ({1- \frac{ \sqrt{2} }{2} }) ==\sqrt{2} - \sqrt{2} + \frac{ \sqrt{2} * \sqrt{2} }{2} } = \frac{2}{2}=1 P. S.sin^2 \frac{x}{2} = \frac{1-cosx}{2}
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years