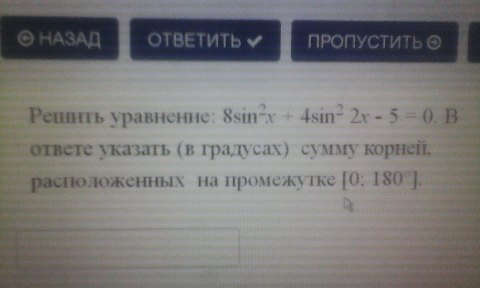
8sin^2x + 4sin^2 *2x - 5=0 . В ответе указать ( в градусах ) сумму корней ,расположенных на промежутке [0,180°]

8sin^2x+16sin^2x*cos^2x-5=08sin^2x+16sin^2x*(1-sin^2x)-5=0sin^2x=y8y+16y-16y^2-5=0-16y^2+24y-5=016y^2-24y+5=0D=256y1=(24+16)/32=40/32=10/8=5/4y2=8/32=1/4sin^2x=5/4sinx=sqrt(5)/2=2,2/2>1 - не вернозначит остается y=1/4sin^2x=1/41) sinx=1/2x1=pi/6+2pi*nx2=5pi/6+2pi*n2) sinx=-1/2x1=-pi/6+2pi*nx2=-5pi/6+2pi*npi/6*(180/pi)=30°5pi/6=150°-pi/6=-30°-5pi/6=-150сумма корней на [0;180°]30°+150°=180°Ответ: 180°

8(sinX)^2+4(sin2x)^2-5=0sin2x=2*sinx*cosx(sin2x)^2=4*(sinx)^2*(cosx)^2=4*(sinx)^2*(1-(sinx)^2)=4*(sinx)^2-4*(sinx)^48(sinX)^2+4*(4*(sinx)^2-4*(sinx)^4)-5=08(sinX)^2+16*(sinx)^2-16*(sinx)^4-5=016*(sinx)^4-24*(sinx)^2+5=04*(sinx)^2=tt^2-6t+5=0D=6^2-4*5=36-20=16t1=(6-4)/2=1t2=(6+4)/2=5(sinx)^2=1/4sinx= -1/2x1=7/6=210°;11/6=330° sinx= 1/2x2=/6=30°; 5/6=150°4(sinx)^2 = 5 (sinx)^2=5/4sinx=√(5/4) > 1  не удовлетворяетsinx=-√(5/4) < -1 не удовлетворяетСумма корней на промежутке [0:180] = 30°+150° = 180°