-
Подскажите, как решать подобное логарифмическое неравенство?
Заранее спасибо за помощь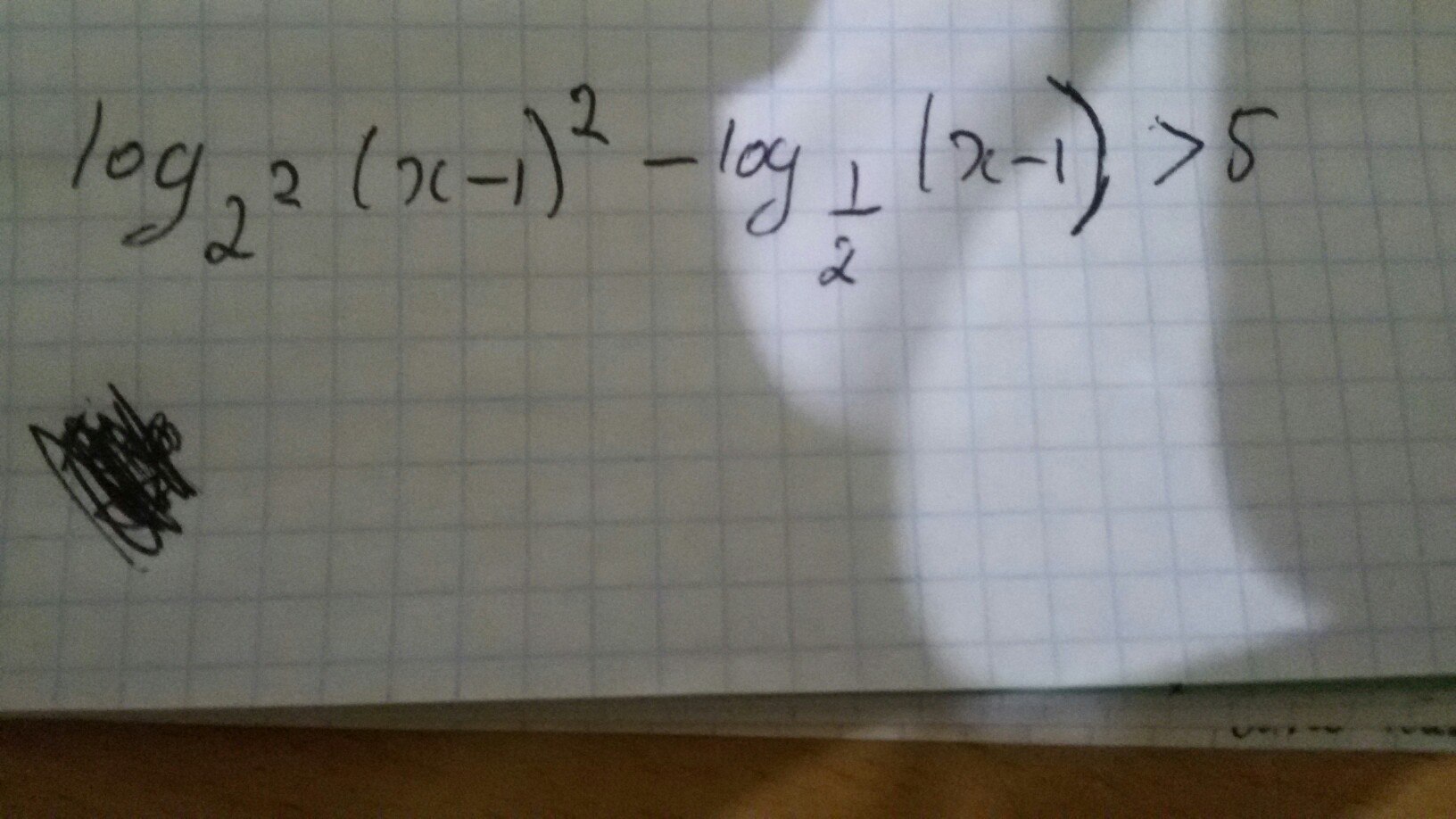
-
Предмет:
Математика -
Автор:
caren - 5 лет назад
-
Ответы 2
Еще вопросы
-
Большенство видов хрящевых рыб обитают в
-
Предмет:
Биология -
Автор:
talonlogan - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
найдите угол между меньшей стороной и диагональю прямоугольника,если он на 70 градусов меньше большего угла между диагоналями
-
Предмет:
Геометрия -
Автор:
jessiesummers - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
К Булычев. Пустой дом. Напишите главных героев произведения.
-
Предмет:
Литература -
Автор:
cheyennelarson - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
С вершины наклонной плоскости высотой 3,5 м, переходящей в " мертвую " петлю радиусом 1 м, соскальзывает без трения шайба. Найти отношение максимальной силы давления шайбы на поверхность " мертвой " петли к минимальной.
-
Предмет:
Физика -
Автор:
bryantuppq - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
