-
Прошу объясните КАК решать подобные примеры.
Всего примеров 10.
Нужен ответ и пояснить как его получили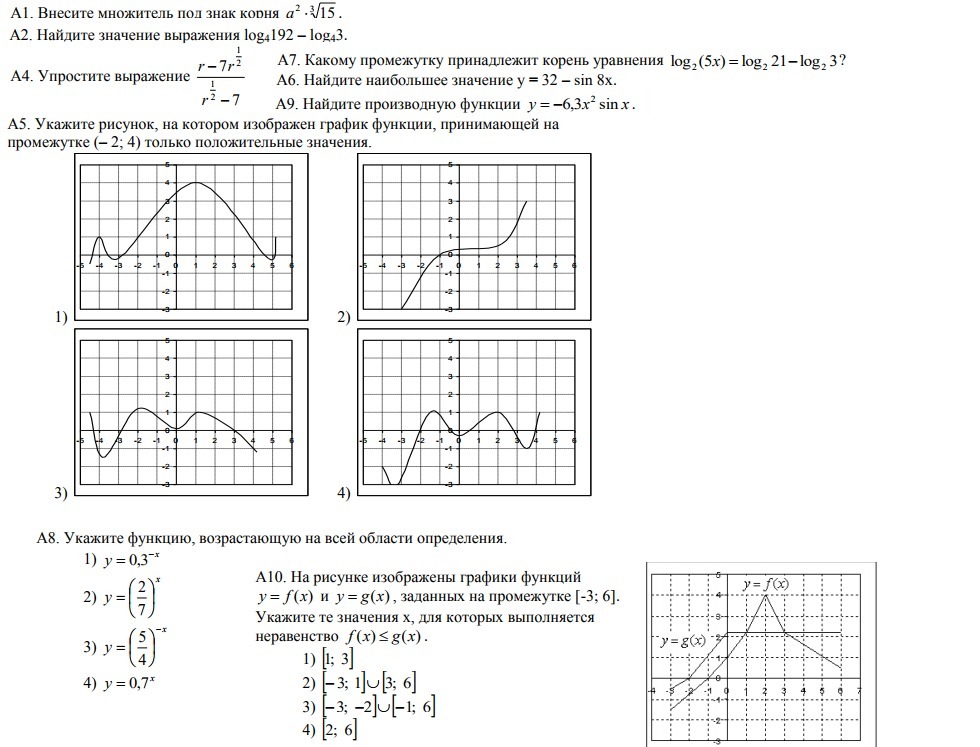
-
Предмет:
Математика -
Автор:
sweet-peateed - 6 лет назад
-
Ответы 3
-
A1 если место а будет цифра то что делать с ним?
-
Автор:
kaidenpeters - 6 лет назад
-
0
-
-
ровно то же самое. возводите в степень число и заносите под корень. числа под корнем в свою очередь так же перемножаются. разница лишь в том, что под знаком корня в этом случае будет не выражение вроде "a^6*15", а просто большее число
-
Автор:
enrique - 6 лет назад
-
0
-
-
объясняю я не очень, но все же попробую.A1. чтобы внести множитель под корень необходимо возвести этот самый множитель в степень корня.на примере:
возводится в 3ю степень :
и в таком виде отправляется под корень:
A2. применение свойств логарифмов. Их нужно знать, чтобы понимать и доводить такие вот выражения до благопристойного вида:в примере необходимо применить следующее свойство:
A3. как я уже и говорила, умение представить градусную меру угла в виде суммы или разности и формулы приведения.A4. степени и их свойства. в данном примере у нас следующее из них:
поэтому представим х как
далее, вынесем
и получим выражение:
скобки сокращаются, остается
, к слову возведение в степень "1\2" равносильно извлечение квадратного корня.A5. положительные значения - это та часть графика, которая расположена выше оси OX; в примере это 1ая функция. (отрицательные значения функция принимает на тех промежутках, где ее график расположен ниже оси OX).A6. значения синуса принадлежат отрезку [-1;1], анализируйте. Максимальное значение функции будет достигнуто при sin8x = -1 и будет равно 32-(-1) = 33A7. логарифмы и их свойства. снова. и к сожалению опять то же самое свойства вычитания логарифмов применять будем:
A8. при возведении в отрицательную степень число или дробь переворачивается. 1.
>0, ⇒ функция будет возрастатьА9. y`=
А10. ориентируемся по графику. ответ 2
-
Автор:
jameson - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Укажите имена существительные мужского рода. 1 – авеню 2 – радио 3 – шампун 4 – тюль 5 – торнадо 6 – спираль 7 – депо
-
Предмет:
Русский язык -
Автор:
kaylen - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
На гладкой горизонтальной поверхности лежит доска, а на ней находится брусок с
массой в n раз меньшей массы доски. Между бруском и доской – трение. Горизонтальная
сила, величина которой прямо пропорциональна времени ее действия, один раз приложена
к доске, другой раз – к бруску. Найдите, во сколько раз раньше начнется проскальзывание
бруска относительно доски во втором случае, чем в первом.-
Предмет:
Физика -
Автор:
krystalcscc - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Четверть куска ленты разрезали пополам. Какую часть всей ленты составляет это половина?
-
Предмет:
Математика -
Автор:
zara85 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Половины груши разрезали пополам. Какая часть все груши составляет это половина?
-
Предмет:
Математика -
Автор:
princevaughan - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
