Найдите площадь фигуры , ограниченной заданными линиями.
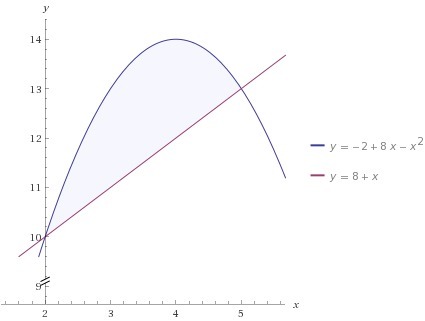
y=8x-x^2-2
y=x+8

ищем пределы интегрирования:8x-x^2-2=x+8 \\x^2-7x+10=0 \\D=49-40=9=3^2 \\x_1= \frac{7+3}{2} =5 \\x_2=2А теперь находим площадь с помощью определенного интеграла:S(G)= \int\limits^5_2 {((8x-x^2-2)-(x+8))} \, dx =\int\limits^5_2 {(7x-x^2-10)} \,dx= \\= (\frac{7x^2}{2} - \frac{x^3}{3} -10x)\int\limits^5_2= \frac{7*25}{2} - \frac{125}{3}-50-(14- \frac{8}{3} -20)= \\=\frac{525-250}{6} -50-14+ \frac{8}{3} +20= \frac{275}{6}+ \frac{8}{3} -44= \frac{275+16}{6} -44= \\=48,5-44=4,5Ответ: 4,5 ед²