-
Алгебра - логарифмическое неравенство по переменному основанию. Помогите пожалуйста!
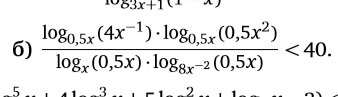
-
Предмет:
Математика -
Автор:
mac97 - 5 лет назад
-
Ответы 6
-
а почему после -3 < 1 / log(2, 0.5x) < 3 знаки поменялись?
-
Автор:
deandredeleon - 5 лет назад
-
0
-
-
Разве они поменялись?
-
Автор:
mercedesmeyers - 5 лет назад
-
0
-
-
ну, -3 превратилась в 1/3, а 3 в -1/3
-
Автор:
figaroutlu - 5 лет назад
-
0
-
-
это как
-
Автор:
jesset9nb - 5 лет назад
-
0
-
-
Я же решаю |1/t| < 3. Это тоже самое, что и |t| > 1/3
-
Автор:
holdenreeves - 5 лет назад
-
0
-
-
Рисуем ОДЗ:0.5x > 0; 0.5x ≠ 1; x > 0; x ≠ 1; 8x^-2 > 0; 8x^-2 ≠ 1; 4x^-1 > 0; 0.5x^2 > 0x > 0; x ≠ 1; x ≠ 2; x ≠ 2√2Делаем крокодилов менее страшными:log(0.5x, 4x^-1) = log(0.5x, 2 * (0.5x)^-1) = log(0.5x, 2) - 1log(0.5x, 0.5x^2) = log(0.5x, 2 * (0.5x)^2) = log(0.5x, 2) + 21 / log(x, 0.5x) = log(0.5x, x) = log(0.5x, 2 * 0.5x) = log(0.5x, 2) + 11 / log(8x^-2, 0.5x) = log(0.5x, 8x^-2) = log(0.5x, 2 * (0.5x)^-2) = log(0.5x, 2) - 2Все логарифмы выразились через log(0.5x, 2). Меняем этот логарифм на t и получаем относительно красивое неравенство:(t - 1)(t + 2)(t + 1)(t - 2) < 40(t^2 - 1)(t^2 - 4) < 40t^4 - 5t^2 - 36 < 0(t^2 - 9)(t^2 + 4) < 0t^2 - 9 < 0t^2 < 9-3 < t < 3 Обидно, но придётся вернуться к логарифму. Сразу поменяем log(0.5x, 2) на 1 / log(2, 0.5x), так веселее.-3 < 1 / log(2, 0.5x) < 3log(2, 0.5x) > 1/3 или log(2, 0.5x) < -1/30.5x > 2^(1/3) или 0 < 0.5x < 2^(-1/3)x > 2^(4/3) или 0 < x < 2^(2/3)Внезапно вспоминаем, что у нас выписано ОДЗ. Радуясь, что мы про него не забыли, выписываем ответ.
Ура!
-
Автор:
semaj - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Пословица к произведению мцыри Лермонтова
-
Предмет:
Литература -
Автор:
siro - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Ханс Христиан Андерсен история одной матери написать краткий рассказ и отзыв о том что учит эта сказка
-
Предмет:
Литература -
Автор:
constancio - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
История Казахстана! Возможно ли было создание социалистического хозяйства в казахском ауле при сохранении кочевого и полукочевого образа жизни?
-
Предмет:
История -
Автор:
tanglescrwi - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Проблемный вопрос продавец воздуха
-
Предмет:
Литература -
Автор:
dollysiwl - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
