-
Решите логарифмические неравенства , с решением
Пожалуйста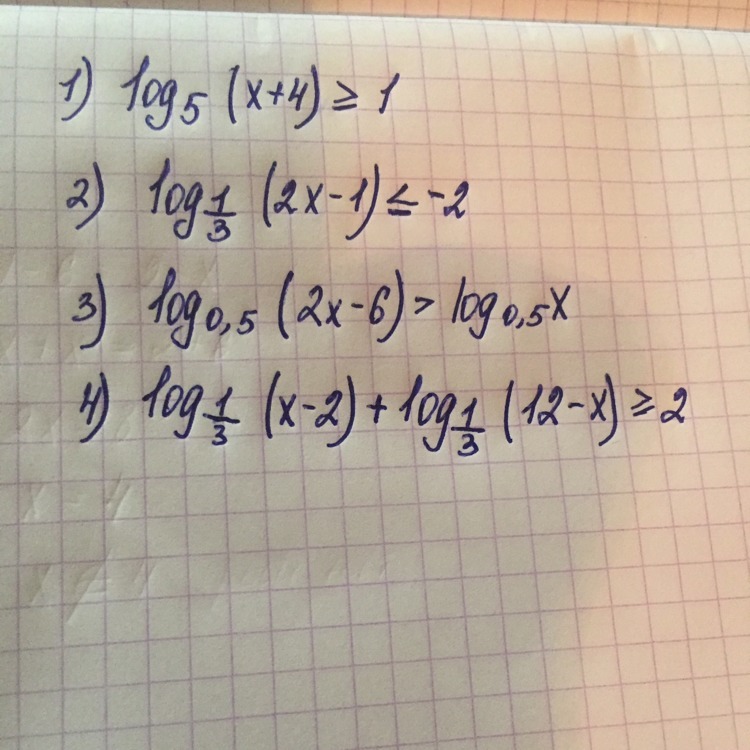
-
Предмет:
Математика -
Автор:
dean7 - 5 лет назад
-
Ответы 2
-
Не туда нажал... сейчас дополню!!!
-
Автор:
liu - 5 лет назад
-
0
-
-
Одз:х+4>0x>-4x∈(-4;+∞)
x+4≥5x≥1Ответ: х∈[1;+∞)
Одз:2х-1>02x>1x>1/2x∈(1/2;+∞)
2x-1≥9 (знак неравенства поменялся, т.к. основание логарифма меньше единицы)2х≥10х≥5Ответ: х≥5, х∈[5;+∞)
Одз:2х-6>02x>6x>3x∈(3;+∞)2x-6<x (знак меняется на противоположный, если основание меньше 1)х<6x<6Ответ: х∈(3;6)
ОДЗ:х-2>0 12-x>0x>2 -x>-12 x<12x∈(2;12)
-x²+14x-24-1/9≤0x²-14x+24+1/9≥0D=196-4(-1)*(-215/9)=196-(860/9)=904/9x1=(-14+√(904/9))/(-2)=7-(4√14)/3 x2=(-14-√(904/9))/(-2)=7+(4√14)/3Ответ: х∈(2;7-(4√14)/3)]∪[7+(4√14)/3;12)
-
Автор:
chippyjacobs - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
о чем рассказывается в произведении горького "В ЛЮДЯХ"
-
Предмет:
Литература -
Автор:
mariyah - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
3x^2 + 4x - 4 = 0
(^ - степень)-
Предмет:
Алгебра -
Автор:
averywillis - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
Первая машинистка печатает 8 страниц в час, а вторая за 4 часа печатает столько же страниц, сколько первая за 3 часа. Сколько страниц отпечатают обе машинистки за 11 часов совместной работы?
-
Предмет:
Математика -
Автор:
tatiana - 5 лет назад
-
Ответов:
5 -
Смотреть
-
-
какой из данных ниже чисел принадлежит отрезку [7;8]?
1) 69/11
2) 80/11
3) 90/11
4) 92/11
если можно с пояснением
How much to ban the user?
1 hour
1 day
100 years
