Задать вопрос Регистрация
Помочь другим

  • Решите пожалуйста
    с подробным решением с очень подробным и с ответом ,даю 100 баллов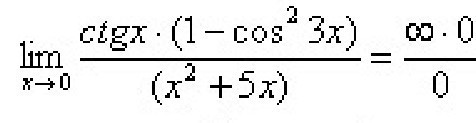

    question img

Ответы 2

  • Начиная с какого места в строчке ctg x (1 - cos^2(3x))/(x^2 + 5x) ~ 1/x * 9x^2 / (x (x + 5)) = 9 / (x + 5) становится непонятно?

    • Автор:

      boyle
    • 5 лет назад
    • 0
  • Используем эквивалентные функции (две функции называются эквивалентными, если предел их отношения равен 1. Это записывается так: f ~ g)ctg x = cos x / sin x ~ 1/x (следствие из первого замечательного предела)1 - cos^2(3x) = sin^2(3x) ~ (3x)^2 (тоже из первого замечательного предела)ctg x (1 - cos^2(3x))/(x^2 + 5x) ~ 1/x * 9x^2 / (x (x + 5)) = 9 / (x + 5)\displaystyle \lim_{x\to0}\frac{\mathrm{\mathop{ctg}}x(1-\cos^23x)}{x^2+5x}=\lim_{x\to0}\frac9{x+5}=\frac9{0+5}=\frac9{5}_______________________\displaystyle \lim_{x\to0}\frac{\mathop{\mathrm{ctg}}x\,(1-\cos^23x)}{x^2+5x}=\lim_{x\to0}\frac{\cos x\cdot\sin^23x}{\sin x\cdot x(x+5)}=\lim_{x\to0}\frac{9\cos x}{x+5}\cdot\frac{x}{\sin x}\times\\\times \left(\frac{\sin 3x}{3x}ight)^2=\lim_{x\to0}\frac{9\cos x}{x+5}\cdot\lim_{x\to0}\frac x{\sin x}\cdot\left(\lim_{3x\to0}\frac{\sin 3x}{3x}ight)^2=\frac{9\cos0}{0+5}\times\\\times1\cdot1^2=\frac95Основное тригонометрическое тождество: sin^2(x) + cos^2(x) = 1Определение ctg x: ctg x = cos x /  sin xПервый замечательный предел: lim sin x / x = 1

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years