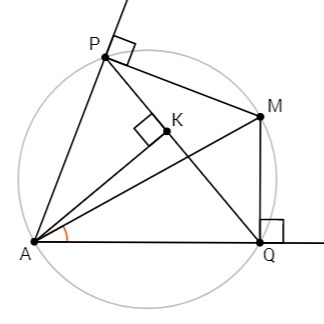
Из точки M, лежащей внутри данного угла с вершиной A, опущены перпендикуляры MP и MQ на стороны угла. Из точки A опущен перпендикуляр AK на отрезок PQ (луч AK лежит между сторонами угла MAP). Известно, что ∠MAK=10∘, ∠MAP=40∘. Найдите градусную величину ∠MAQ.

APMQ - вписанный четырехугольник (∠APM=∠AQM=90, сумма противоположных углов равна 180).∠MAQ=∠MPQ (вписанные углы, опирающиеся на дугу MQ)∠MPQ=90-∠APK∠APK=90-∠KAP (△APK)∠KAP= ∠MAP-∠MAK =40-10 =30∠MAQ= 90-(90-∠KAP) =∠KAP =30