-
Исследовать данную функцию методами дифференциального исчисления и построить их графики. y=x/(x2+1)
Исследование функции рекомендуется проводить по следующей схеме:
1) найти область определения функции;
2) исследовать функцию на непрерывность;
3) определить, является ли данная функция четной, нечетной;
4) найти интервалы монотонности функциии точки ее экстремума;
5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба;
6) найти асимптоты графика функции.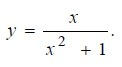
-
Предмет:
Математика -
Автор:
rosebud4pcx - 5 лет назад
-
Ответы 1
-
ДАНОY = x/(x²+1)ИССЛЕДОВАНИЕ1. Область определения - X∈(-∞;+∞) 2.Непрерывная - разрывов нет.Пересечение с осью Х.У=0 → х = 0.3. Исследование на чётность.Y(-x) = - x/(x²+1) = - Y(x) - функция нечётная.4. Интервалы монотонностиПервая производная функцииY'(x) = 1/(x²+1) - 2x²/(x²+1)²Корни первой производнойY'(x)=0 → x = -1 и х = 1 - точки экстремума.Возрастает - X∈[-1;1]Убывает - Х∈(-∞1]∪[1;+∞)Минимум - Y(-1) = - 0.5Максимум - Y(1) = 0.5 5. Исследование на перегибы.Вторая производная функции - Y"(x) = (2x³-6x)/(x⁶+3x⁴+3x²+1)Точка перегиба - Y"(x)=0 при Х=0.Вогнутая - "ложка" - Х∈(-∞;0]Выпуклая - "горка" - Х∈[0;+∞) 6. Наклонная асимптота - Y= 0.7. График прилагается.

-
Автор:
oreotrxa - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- раскройте скобки и приведите подобные слогаемые 3x(x-5)-5x(x+3)
-
рабочие должны заасфальтировать 45m велосипеди на дорожке одну пятую часть дорожки не уже заасфальтировали сколько метров велосипеде на дорожке осталось заасфальтировать
-
Предмет:
Математика -
Автор:
jaime - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
реши уравнение 4*x=28+52
-
Предмет:
Математика -
Автор:
concepciónivai - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Срочно помогите.
Найти значение выражения. x=16; y=25
[tex] \frac{x-y}{x^ \frac{1}{2}-y^ \frac{1}{2}}+ \frac{y^ \frac{1}{2}-y}{y \frac{1}{2} }[/tex]
How much to ban the user?
1 hour
1 day
100 years
