Задать вопрос Регистрация
Помочь другим

  • помогите решить интеграл1111111111111
    ((e^(x/2))/(sqrt(e^x-1)))*dx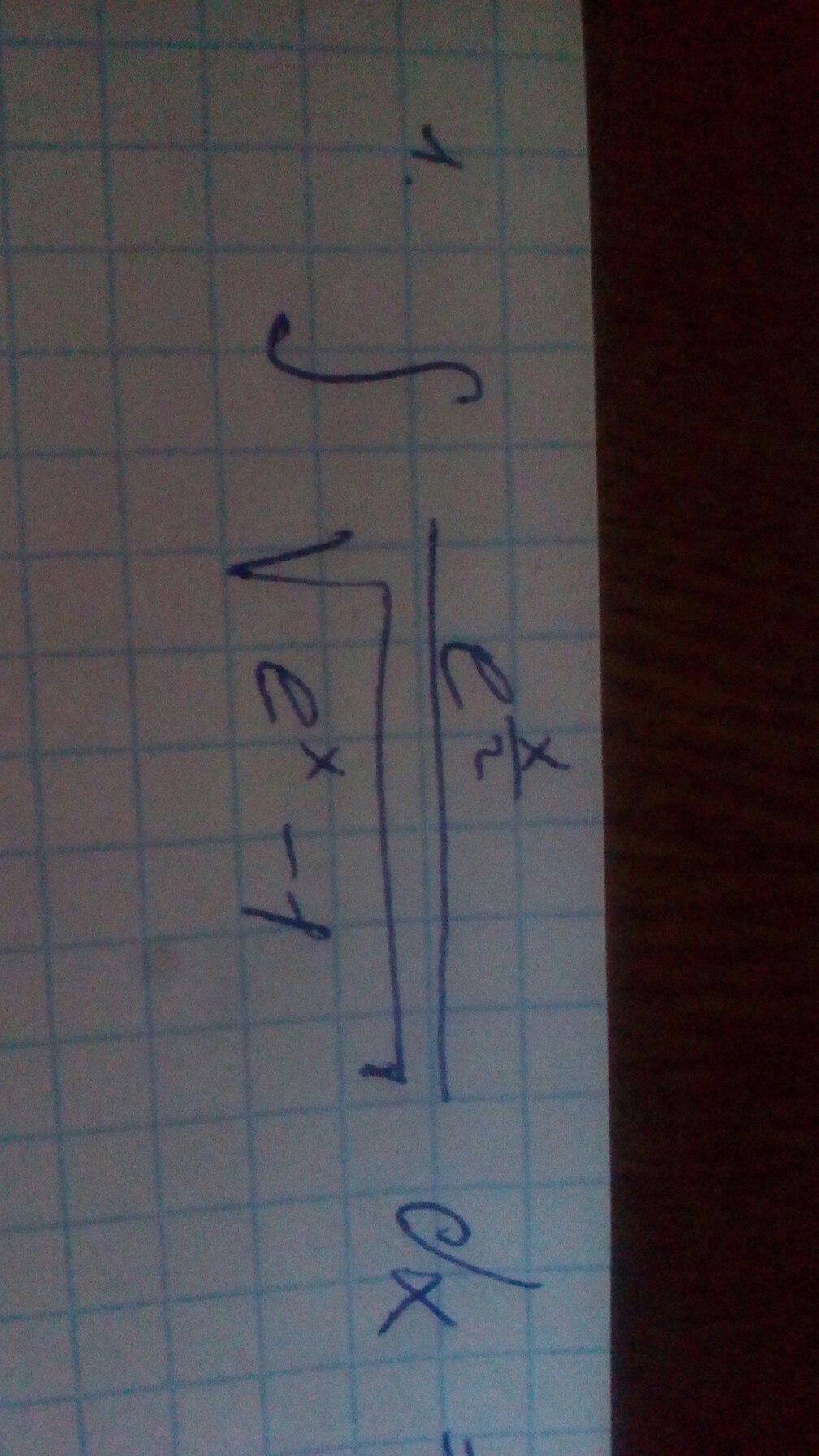

    question img

Ответы 4

  • как ты перешёл от e^(x/2) к 2e^u?

    • Автор:

      annutb3
    • 4 года назад
    • 0
  • применил замену u=x/2
  • спасибо
  • \int \frac{e^{\frac{x}{2}}}{\sqrt{e^x-1}}dx=\int \frac{2e^u}{\sqrt{e^{2u}-1}}du=2\cdot \int \:\frac{e^u}{\sqrt{e^{2u}-1}}du=2\cdot \int \:\frac{1}{\sqrt{v^2+1}}dv= \\ =2\ln \left|\sqrt{v^2+1}+vight|=2\ln \left|\sqrt{\left(\sqrt{e^{2\cdot \frac{x}{2}}-1}ight)^2+1}+\sqrt{e^{2\cdot \frac{x}{2}}-1}ight|= \\ =2\ln \left|e^{\frac{x}{2}}+\sqrt{e^x-1}ight| \\ OTBET : \boxed{2\ln \left|e^{\frac{x}{2}}+\sqrt{e^x-1}ight|+C}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years