Задать вопрос Регистрация
Помочь другим

  • Помогите решить диф. уравнение методом Бернули (y=uV; y'=u'V+uv')

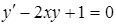
    question img

Ответы 1

  • y'-2xy+1=0y'-2xy=-1Вводим замену:y=uvДифференцируем:y'=u'v+uv'Подставляем в наше уравнение выражения для y и y'.u'v+uv'-2xuv=-1Выносим u за скобкиu'v+u(v'-2xv)=-1v'-2xv=0 \frac{dv}{v}-2xdx=0 \int\limits{\frac{dv}{v} } - \int\limits2xdx=0 ln|v|-2* \frac{x^2}{2}=c c=0ln|v|=x^2v=e^{x^{2}} \frac{du}{dx}*e^{x^2} =-1du=-e^{-x^2}dxu= -\int\limits e^{-x^2}+c \int\limits e^{-x^2}dx=[z= \sqrt{2}x; x^2= \frac{z^2}{2}; dx= \frac{1}{ \sqrt{2} }dz]= \int\limits e^{ -\frac{z^2}{2} }* \frac{1}{ \sqrt{2} }dz= \frac{1}{ \sqrt{2} } \int\limits e^{- \frac{z^2}{2} }dz= \frac{ \sqrt{2 \pi } }{ \sqrt{2}} Ф(z)+c= \sqrt{ \pi } Ф( \sqrt{2}x )+cu=- \sqrt{ \pi }Ф( \sqrt{2}x )+cy=uv=(- \sqrt{ \pi } Ф( \sqrt{2} x)+c)e^{x^2}=- \sqrt{ \pi }e^{x^2} Ф( \sqrt{2}x )+ce^{x^2}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years