-
Решение по пунктам
Очень нужно
У самой мозгов не хватает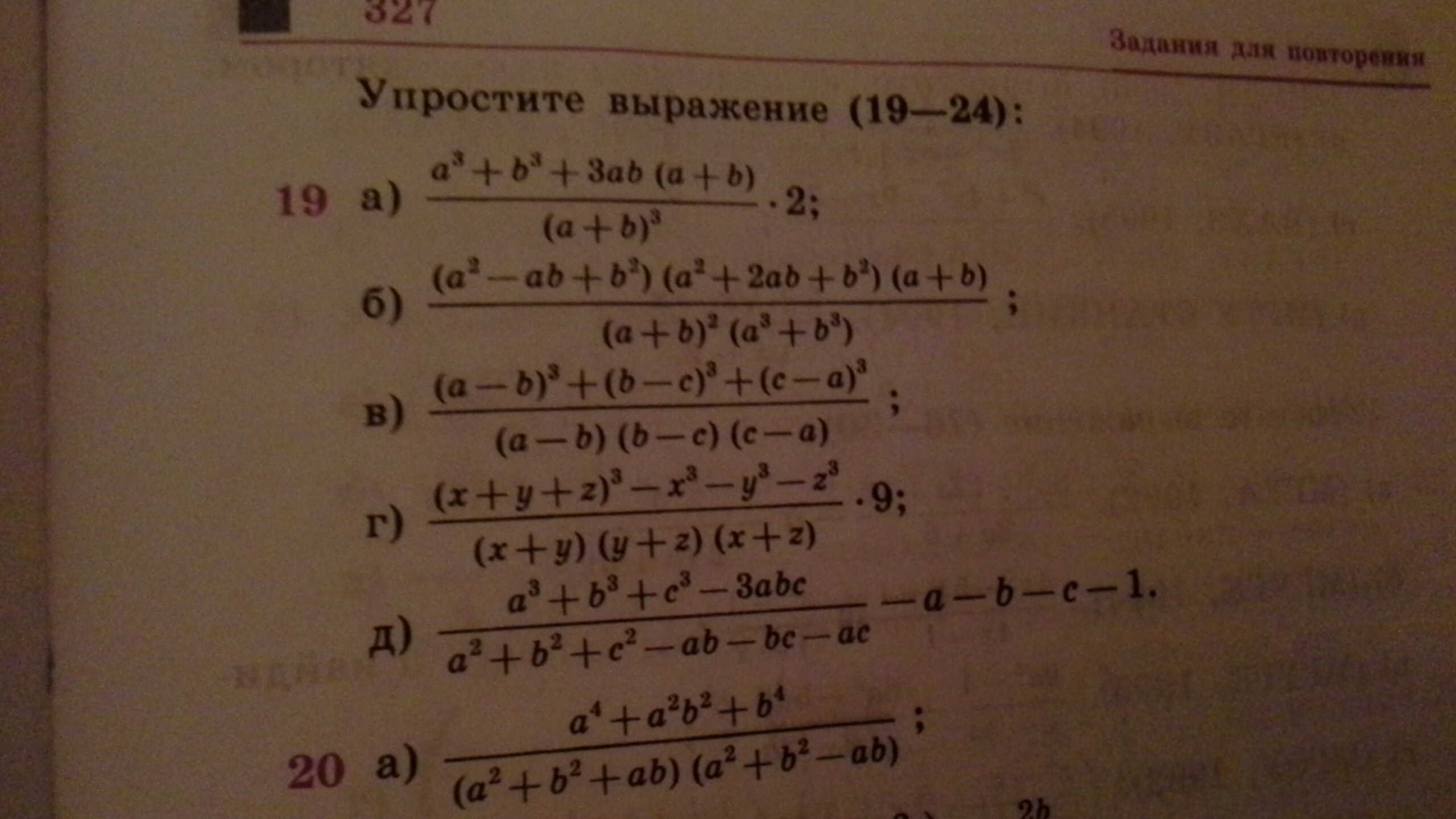
-
Предмет:
Математика -
Автор:
dempseyr5fv - 5 лет назад
-
Ответы 2
-
Сможешь решить ещё один норме, я его в общую сейчас скину?
-
Автор:
lillianti9b - 5 лет назад
-
0
-
-
-
Автор:
baileydo0q - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Текст о друге по английскому 4 класс
-
Предмет:
Английский язык -
Автор:
delgado - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
"Зачем я еду, с чего я взял." "Ну, (имя и фамилия человека), ну милая, ну откройте пожалуйста!" Можно ли так писать? Это считается ошибкой? Повтор одного и того же слова в одном предложении.
-
Предмет:
Литература -
Автор:
moonshine6 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
текст
Когда я был маленьким,во всех домах ещё стояли печки. Дрова были разные: берёзовые, сосновые, осина...И перепутать зап...хи дымков было совершенно невозможно.
Отправляя меня куда-то ,бабушка НАКАЗЫВАЛА:
-Не заблудись!Идёшь сначала на запах елового дыма, в переулке сворачиваешь на осиновый и шагаешь ,пока не запахнет берёзой...А наш родной запах...
-Да, знаю,знаю! -отвечал я бабушке. - Свежие пироги с капустой.
выбери из данных предложений главную мысль текста и отметьте её галочкой.
родной запах поможет найти дорогу домой.
какие вкусные у бабушки пироги!
я уже не маленький, не заблужусь.
перепутать запахи дымков было совершенно не возможно.
объясните значение выделенного в тексте слова?
-
Предмет:
Русский язык -
Автор:
pepper - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Чем является солнечное в : значении в жизни человека
-
Предмет:
Биология -
Автор:
willieizd3 - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
