Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста
    ВЫЧИСЛИТЬ ПРЕДЕЛ ФУНКЦИИ
    Примеры на фото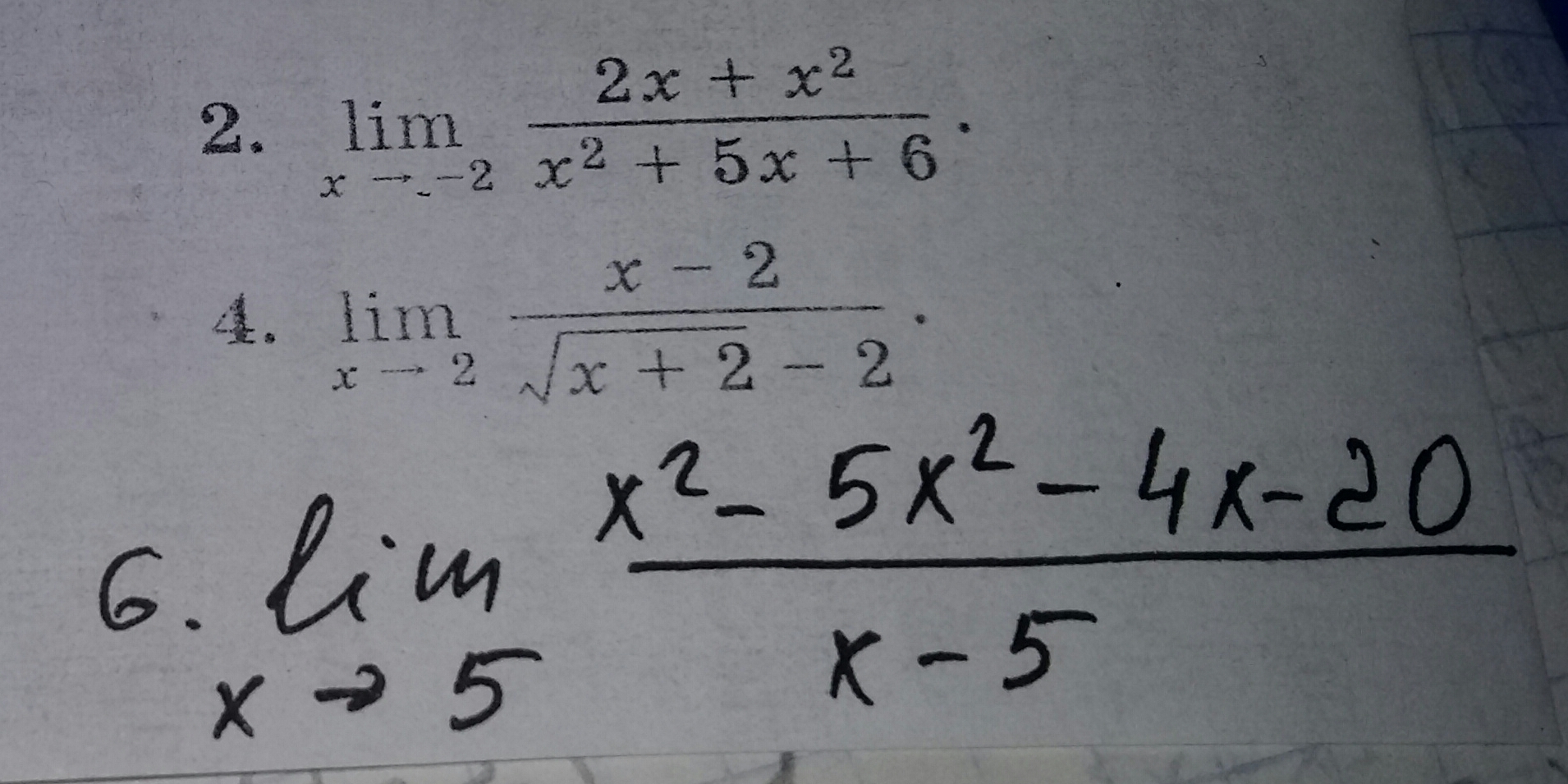

    question img

Ответы 1

  • \lim_{x \to 5}\frac{ x^{3}- 5x^{2} -4x+20 }{x-5}= \lim_{x \to 5} \frac{ x^{2} *(x-5)-4*(x-5)}{x-5} = \lim_{x \to 5} \frac{(x-5)*( x^{2} -4)}{x-5} \lim_{x \to -2} \frac{2x+ x^{2} }{ x^{2} +5x+6} = \frac{2*(-2)+ (-2)^{2} }{ (-2)^{2}+5*(-2)+6 } = \frac{0}{0} неопределенность вида : 0/0 \lim_{x \to -2} \frac{2x+ x^{2} }{ x^{2} +5x+6} = \lim_{x \to -2} \frac{x*(2+x)}{(x+2)*(x+3)} = \lim_{x \to -2} \frac{x}{x+3} = \frac{-2}{-2+3} =-2 \lim_{x \to 2} \frac{x-2}{ \sqrt{x+2}-2 } = \frac{2-2}{ \sqrt{2+2} -2}= \frac{0}{0} \lim_{x \to 2} \frac{(x-2)*( \sqrt{x+2}+2 )}{( \sqrt{x+2}-2 )*( \sqrt{x+2}+2 )} = \lim_{x \to 2} \frac{(x-2)*( \sqrt{x+2}+2 )}{ ( \sqrt{x+2} )^{2} - 2^{2} } == \lim_{x \to 2} \frac{(x-2)*( \sqrt{x+2}+2 )}{x+2-4}= \lim_{x \to 2} \frac{(x-2)*( \sqrt{x+2}+2 )}{x-2} == \lim_{x \to 2} ( \sqrt{x+2}+2 )= \sqrt{2+2}+2=4 пример № 6 "подредактирую условие", чтобы "красиво решилось" \lim_{x \to 5} \frac{ x^{3}-5 x^{2} -4x +20}{x-5} = \lim_{x \to 5} \frac{ x^{2} *(x-5)-4*(x-5)}{x-5} = \lim_{x \to5} \frac{(x-5)*( x^{2} -4)}{x-5} = \lim_{x \to 5} ( x^{2} -4) = 5^{2}-4=25-4=21

    • Автор:

      talan
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years