-
Детально объясните эквивалентные переходы в уже готовом решении. Особенно интересуют последние 4 строчки решения, максимально подробно распишите. Задание (доказать методом математической индукции) и решение на картинках ниже:
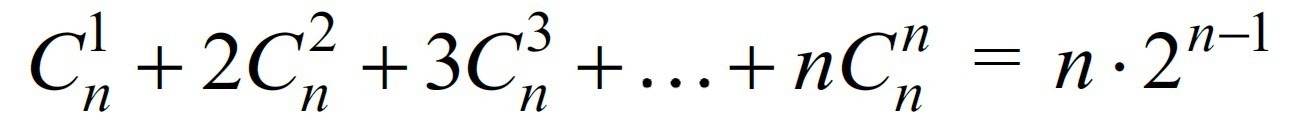

-
Предмет:
Математика -
Автор:
sofíand8r - 5 лет назад
-
Ответы 6
-
Ок, время есть.
-
Автор:
big guybtym - 5 лет назад
-
0
-
-
Как там, появились идеи?
-
Автор:
oscarkmpv - 5 лет назад
-
0
-
-
Да, я упустил k+1, можешь дописать. В доказательстве твоём видно на 3 строчке какие коэффициенты мы складываем kC^(k) + (1+k)C^(k). Тут показали лучше, что C^(k+1) [индексы тут я не напишу] будет равно (k+1)C^k, тут это не доказывали через факториалы а просто показали наглядно, а дальше обычная математика. Вот и всё, в 5 часов ночи я пытался тоже что-то такое показать, но упоролся)
-
Автор:
clicker - 5 лет назад
-
0
-
-
В том то и дело, что я не понимаю этой обычной математики в том решении, а в этом задании просил просто расписать переходы последних 4-х строчек более подробно.
-
Автор:
ellezyzn - 5 лет назад
-
0
-
-
там написано 28+7=2х; x=17.5, а мне нужно 28+7=2x; 35=2x; 2x=35; x=17.5.
-
Автор:
guillermo - 5 лет назад
-
0
-
-
1. Сначала по методу математической индукции мы проверяем это выражение для n = 1 - базисное значение, а потом предполагаем, что равенство равно и для некоторых k элементов. 2. Записываем его для k элементов. 3. Теперь записываем его для шага индукции, то есть для k+1 элементов.
это коэффициент, использующийся в биноме Ньютона. 1 Формула:
тоже взята из свойств бинома Ньютона, а точнее его связи с треугольником Паскаля. 2. Формула:
- это тоже свойство биноминальных коэффициентов, суммирование по k. Так как равеноство
выполняется гарантировано, то теперь запишем для k+1 по-новому:
- по правилу симметрии, которое тут опустили как раз. Получается:
Что и требовалось доказать. Биноминальные коэффициенты и их свойства.
-
Автор:
kittyhood - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
докажите что общение является одним из видов деятельности. приведите примеры не менее трёх доказательств
-
Предмет:
Обществознание -
Автор:
ashanti - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Известно, что сумма чисел x и y равна 1,4, а разность чисел x и y равна 0,2.
Найдите произведение чисел x и y. -
ОПРЕДЕЛИ МАССУ КАЧАНА КАПУСТЫ-НА ЛЕВОЙ СТОРОНЕ ВЕСОВ КАПУСТА РЯДОМ ГИРИ2КГ.НА ПРАВОЙ СТОРОНЕ ВЕСОВ ГИРИ 5 КГ. НА ВЕСАХ ПОКАЗЫВАЕТ ЧТО ВСЁ РОВНО
-
Предмет:
Математика -
Автор:
quinnashley - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Вычислите:
1.2^-3*2/3^-2
2.(-3)^-3
3.35+(1/5)^-2
Заранее спасибо)
How much to ban the user?
1 hour
1 day
100 years
