Задать вопрос Регистрация
Помочь другим

  • Решите пожалуйста !!!
    У меня получилось x=2, y=3 правильно ?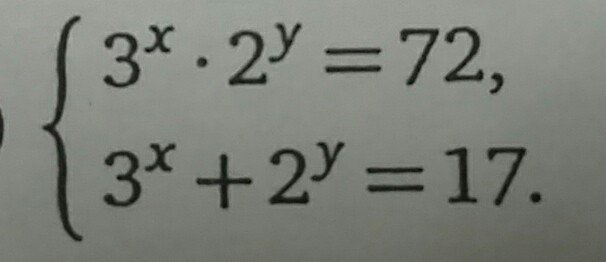

    question img

Ответы 1

  • Пусть t=3 ^{x} ; \\ u=2 ^{y} Система уравнений примет вид \left \{ {{t*u=72} \atop {t+u=17}} ight. Из первого уравнения выразим u=72/t и подставим во второе t+ \frac{72}{t} =17, обе части которого умножим на t:t^{2} +72=17t или t^{2} -17t+72=0Получилось квадратное уравнение. Решаем его через дискриминант:D= 17^{2} -4*1*72=289-288=1Отсюда: t_{1} = \frac{17+ \sqrt{1} }{2*1} =9 \\ t_{2} = \frac{17- \sqrt{1} }{2*1} =8иu_{1} = \frac{72}{9} =8 \\ u_{2} = \frac{72}{8} =9Делаем обратную заменуt _{1} = 3^{x_{1}} =9; x_{1}=2u_{1}=2 ^{y_{1}} =8; y_{1}=3Это одно решение, но есть и второе:t _{2} = 3^{x_{2}} =8; ln3^{x_{2}} =ln8; x_{2}*ln3=ln8; x_{2}= \frac{ln8}{ln3} u _{2} = 2^{y_{2}} =9; ln2^{y_{2}} =ln9; y_{2}*ln2=ln9; y_{2}= \frac{ln9}{ln2} Можно прологарифмировать по другому:t _{2} = 3^{x_{2}} =8; log _{3} 3^{x_{2}} =log _{3}8; x_{2}*log _{3}3=log _{3}8; x_{2}= log _{3}8u _{2} = 2^{y_{2}} =9; log _{2} 3^{x_{2}} =log _{2}9; x_{2}*log _{2}2=log _{2}9; x_{2}= log _{2}9Проверка3 ^{log _{3}8} *2^{log_{2}9}=8*9=72Итак,1) x = 2; y = 32) x=log_{2}9 и  y=log_{3}8

    • Автор:

      juan1j7c
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years