-
Надо найти область определения функции(номера 5.11 и 5.14)
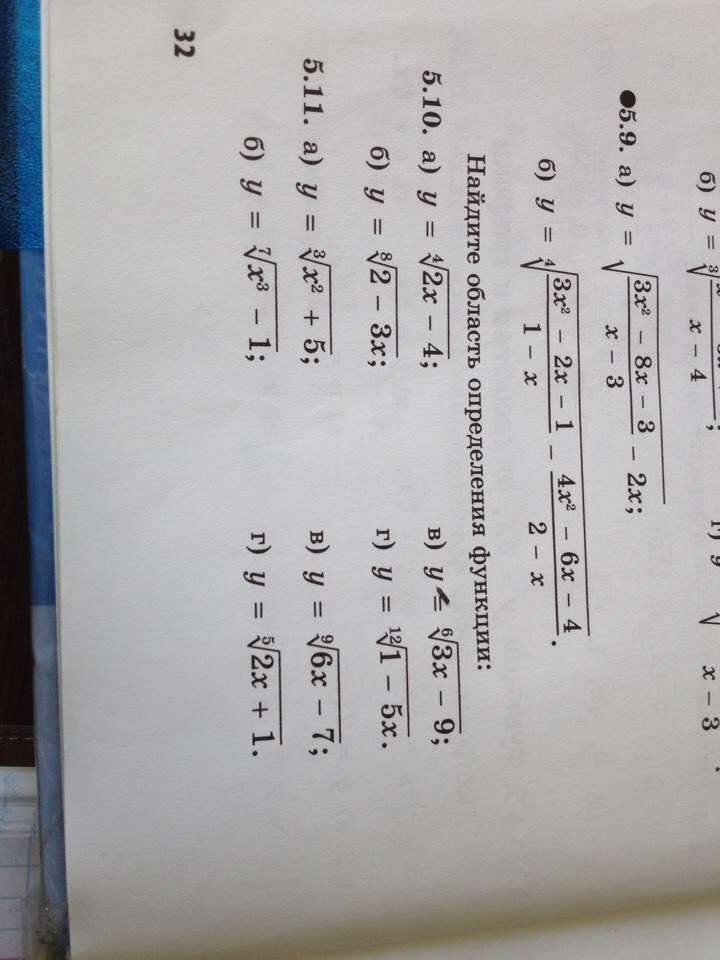
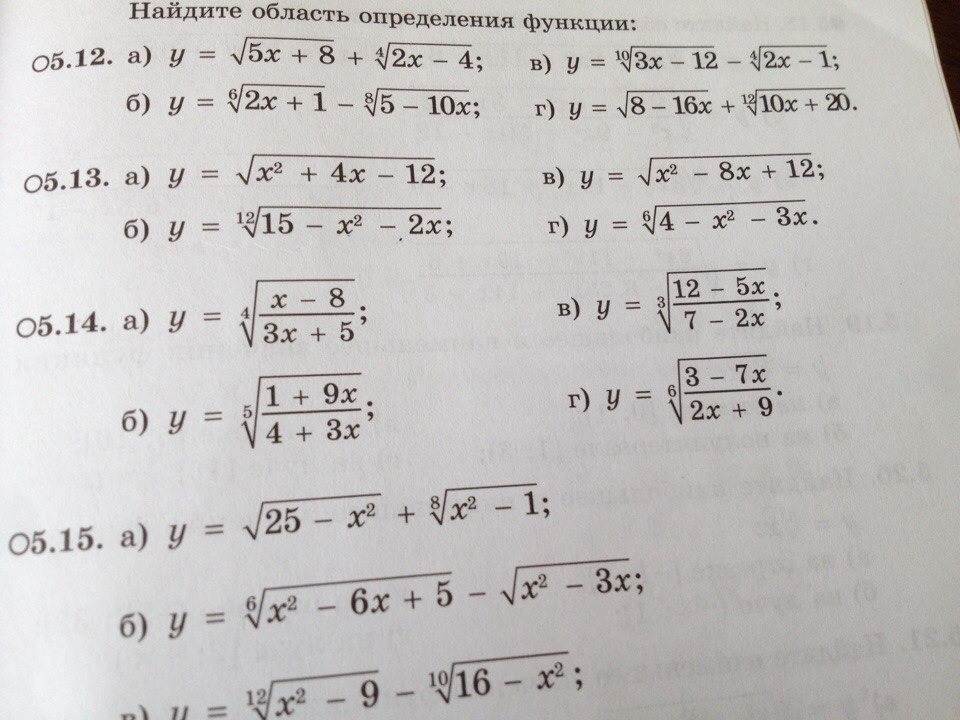
-
Предмет:
Математика -
Автор:
jordanweiss - 5 лет назад
-
Ответы 1
-
Решение, по понятиям.В примере 5,11 Все радикалы НЕЧЕТНОЙ степени - 3,5,7, и 9.И эти радикалы существую при любых значениях.Или в записи для ВСЕХ задач.ОТВЕТ Х∈(-∞;+∞)или словами - все действительные .В примере 5,14. наблюдаем две неприятности.1 - это корни четной степени - не все - отсюда под корнем должно быть неотрицательное число. Х≥ 0.2 - это дроби не должно быть деления на ноль.Разбираем каждый пример ВНИМАТЕЛЬНО.5,14 а) - четная степень (4) - не отрицательный числитель Х-8 ≥ 0 или Х≥ 8 - в числителе - В знаменателе не 0 или3Х+5 ≠ 0 Х ≠ -5/3Объединяем и получаем - 8 включается - квадратная скобка.ОТВЕТ X∈[8;+∞)5.14 б) Нечетная степень (5) - уже проще.4 + 3х ≠ 0 - исключаем деление на 0.х ≠ 4/3 = 1 1/3 - исключаем - КРУГЛЫЕ скобки.ОТВЕТ Х∈(-∞;4/3)∪(4/3;+∞)5,14.в)Исключаем Х = 3,5 - деление на 0 в знаменателе.ОТВЕТ Х∈(-∞;3,5)∪(3,5;+∞)5,14,г)3 - 7х ≥ 0 или х ≤ 3/7 - в знаменателе не отрицательное.2х + 9 ≠ 0х ≠ - 4,5Попробуем правильно объединитьОТВЕТ Х∈(-∞;- 4,5)∪(-4,5; 3/7]
-
Автор:
abby - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите составить текст 7-8 предложений:3
Заранее Спасибо:3-
Предмет:
Русский язык -
Автор:
jetgtc8 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Напишите о характере, душевных качествах близкого, дорого тебе человека.
____________________________________________________________________
Можно использовать эти слова: золотой, солнечный, мягкий, теплый, легкий, безоблачный, открытый-
Предмет:
Русский язык -
Автор:
hannaschroeder - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Масштаб
Определите масштаб плана, если участок площадью 7200м2 изображён на этом плане в виде прямоугольника со сторонами 12 см и 6 см
Заранее спасибо за помощь)-
Предмет:
Математика -
Автор:
alyssamoore - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
напишите числа обратные числам 2;-9; 16,5; -42,5; -50; 71,3
-
Предмет:
Математика -
Автор:
nicolas910y - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
