-
пожалуйста!!!напишите решение.......
Найти общие интегралы уравнений и частные решения дифференциальных уравнений, удовлетворяющие начальным условиям: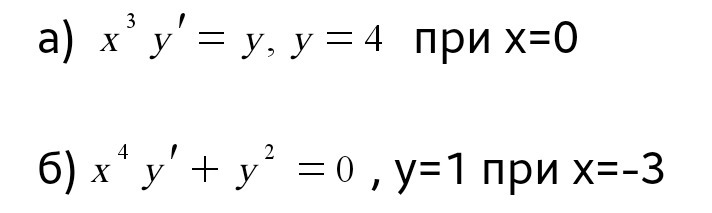
-
Предмет:
Математика -
Автор:
pacheco - 6 лет назад
-
Ответы 1
-
Проверка:
Проверка:
-
Автор:
nicosqrs - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Составить текст рассуждения. Почему осень золотая?(помогите плз^_^)
-
Предмет:
Русский язык -
Автор:
matilda89hk - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Чем отличается Дубровский от Троекурова
Семейными отношениями к как относится крестьянством
И отношения к детям-
Предмет:
Литература -
Автор:
bethanyvega - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- На какой дистанции автомобиль разгонится от скорости 72 км/ч до 144 км/ч, двигаясь с ускорением 2 м/с^2 ? Если можно, то через дано
-
вычислить относительную плотность хлороводородной кислоты HCl по водороду и по воздуху
-
Предмет:
Химия -
Автор:
cuddle pigwgap - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
