Задать вопрос Регистрация
Помочь другим

  • Найдите производные dy/dx данной функции.
    Если знаете хотя бы как начать. буду очень благодарна.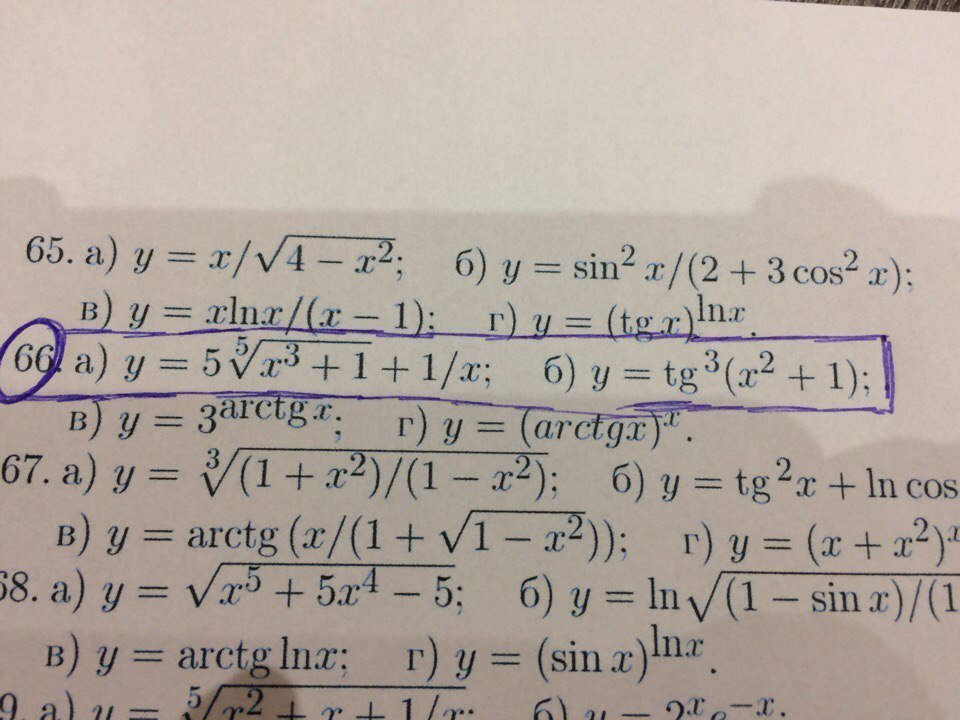

    question img

Ответы 2

  • Большое спасибо. Посмотрите у меня еще задачи, буду очень благодарна.
  • Найдите производные dy/dx данной функции66)a)y=5 \sqrt[5]{x^3+1}+ \frac{1}{x} b)y=tg^3(x^2+1)Решениеa)y'=(5\sqrt[5]{x^3+1}+ \frac{1}{x})'=(5(x^3+1)^{ \frac{1}{5} })'+ (x^{-1})'=5* \frac{1}{5} (x^3+1)^{ \frac{1}{5}-1 }*(x^3+1)'- x^{-2}=(x^3+1)^{ -\frac{4}{5}}*3x^2- \frac{1}{x^2}== \frac{3x^2}{ \sqrt[5]{(x^3+1)^4} }- \frac{1}{x^2} b)y'=(tg^3(x^2+1))'=3tg^2(x^2+1)*(tg(x^2+1))'= 3tg^2(x^2+1)* \frac{1}{cos^2(x^2+1)}*(x^2+1)'=3tg^2(x^2+1)* \frac{1}{cos^2(x^2+1)}*2x= \frac{6xtg^2(x^2+1)}{cos^2(x^2+1)}= \frac{6xsin^2(x^2+1)}{cos^4(x^2+1)}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years