Задать вопрос Регистрация
Помочь другим

  • Найдите пределы функции. Не пользуясь правилом Лопиталя.

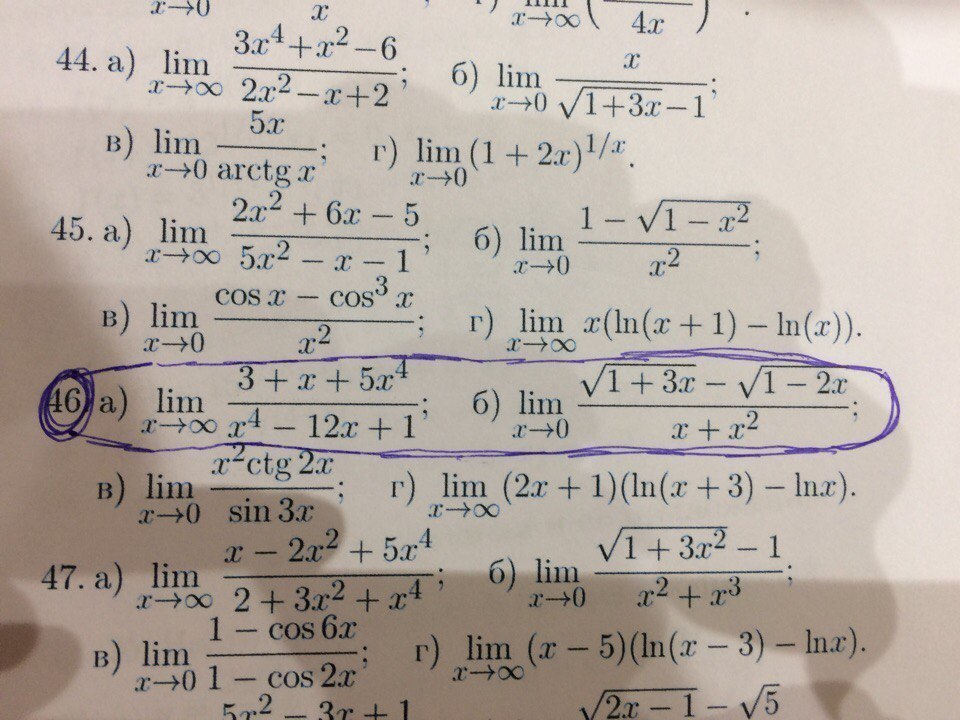
    question img

Ответы 6

  • -12/оо^2 + 1/oo^4. А попробуйте обновить страницу. Бывает не сразу формулы показываеются нормально.
  • это нули? верно?

    • Автор:

      chocolate
    • 5 лет назад
    • 0
  • Нет, это бесконечность. Вместо икса подставляется бесконечность - оо.

    • Автор:

      gordo
    • 5 лет назад
    • 0
  • поняла, спасибо

    • Автор:

      joanerne
    • 5 лет назад
    • 0
  • посмотрите пожалуйста у меня еще задания от сегодняшнего числа, буду очень благодарна.
  • 46a) Неопределённость ∞/∞ раскрываем делением числителя и знаменателя на икс в максимальной степени, т.е. на x^4  \lim_{x \to \infty} \frac{3+x+5 x^{4} }{ x^{4} -12x+1} = \lim_{x \to \infty} \frac{ \frac{3}{x^{4}} + \frac{1}{x^{3}} +5}{ 1 - \frac{12}{x^{3}} + \frac{1}{x^{4}} } =\frac{ \frac{3}{oo^{4}} + \frac{1}{oo^{3}} +5}{ 1 - \frac{12}{oo^{3}} + \frac{1}{oo^{4}} } = \frac{0+0+5}{1-0+0} =546б) Неопределённость 0/0 раскрываем умножением числителя и знаменателя на выражение, сопряжённое числителю, т.е. на ( \sqrt{1+3x}+ \sqrt{1-2x} ) \lim_{x \to \inft0} \frac{( \sqrt{1+3x}- \sqrt{1-2x} )}{x+ x^{2} } = \lim_{x \to \inft0} \frac{( \sqrt{1+3x}- \sqrt{1-2x} )*( \sqrt{1+3x}+ \sqrt{1-2x} )}{x*(1+ x)*( \sqrt{1+3x}+ \sqrt{1-2x} )} } = \\ \\ = \lim_{x \to \inft0} \frac{(1+3x)- (1-2x) }{x*(1+ x)*( \sqrt{1+3x}+ \sqrt{1-2x} )} } = \lim_{x \to \inft0} \frac{5x}{x*(1+ x)*( \sqrt{1+3x}+ \sqrt{1-2x} )} } = \\ \\ = \lim_{x \to \inft0} \frac{5}{(1+ x)*( \sqrt{1+3x}+ \sqrt{1-2x} )} } = \frac{5}{(1+ 0)*( \sqrt{1+3*0}+ \sqrt{1-2*0} )} = = \frac{5}{1*(1+1)} = \frac{5}{2}

    • Автор:

      nikita38
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years