-
Помогите пожалуйста!!!!!!!!
Номер 4 (пункт 2 и 3)
Номер 5 (1,3,4)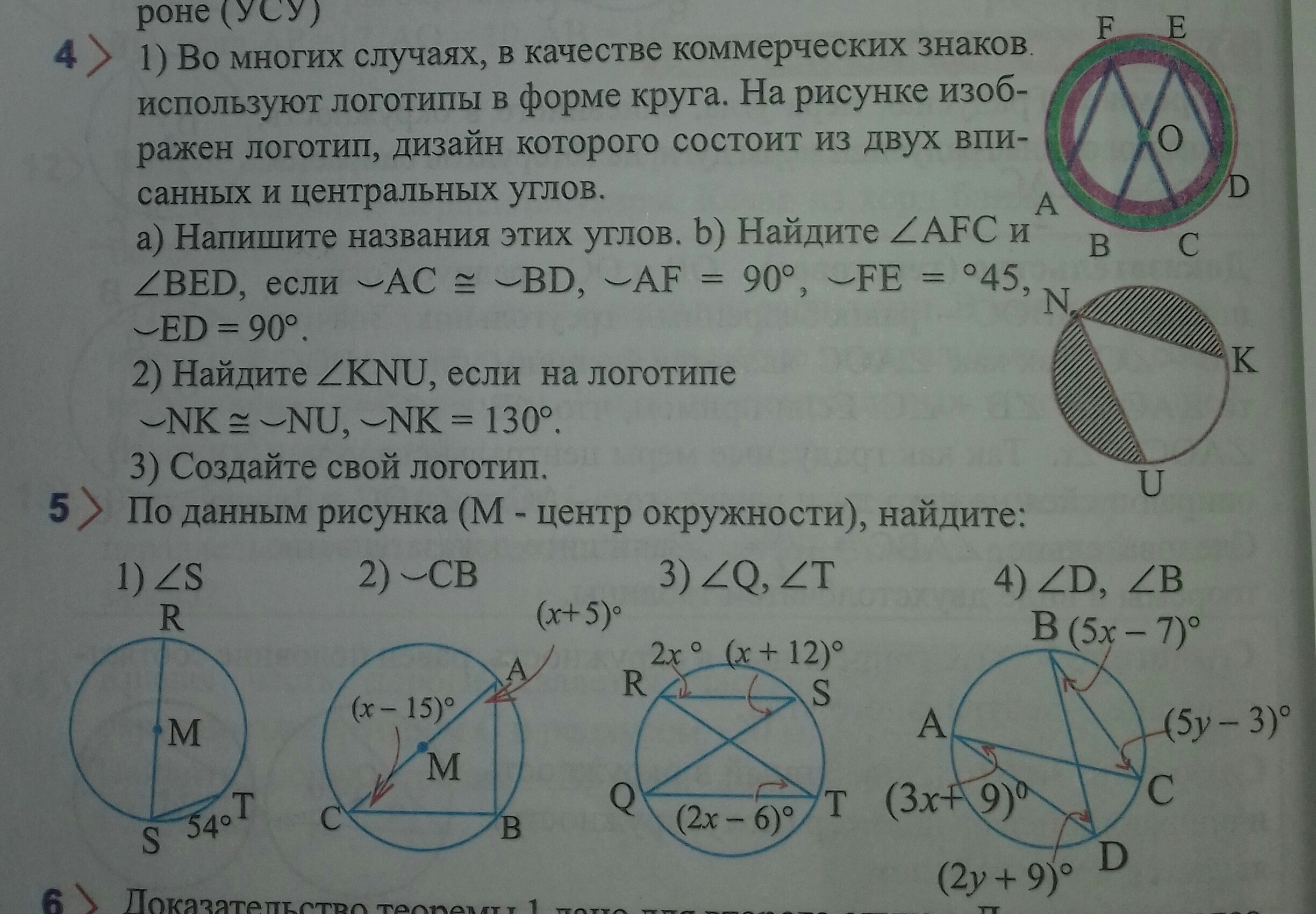
-
Предмет:
Математика -
Автор:
roy13 - 5 лет назад
-
Ответы 6
-
Это логотипы для 3 пункта, да?
-
Автор:
willie - 5 лет назад
-
0
-
-
Ну, типа, да..))
-
Автор:
cheyanne - 5 лет назад
-
0
-
-
спасибо большое)))
-
Автор:
emerson52 - 5 лет назад
-
0
-
-
Да не за что..)) Удачи!
-
Автор:
hamlet - 5 лет назад
-
0
-
-
спасибо))
-
Автор:
marín29 - 5 лет назад
-
0
-
-
4) 2. Полная окружность 360° Так как NK = NU = 130°, то NK+NU = 260° и оставшаяся часть дуги: 360 - 260 = 100° Угол KNU - вписанный. Величина вписанного в окружность угла равна половине дуги окружности, на которую он опирается. Тогда ∠KNU = 1/2 * 100 = 50°5) 1. Так как RS - диаметр, то ∠RTS = 90°. Угол ∠SRT - вписанный, его величина равна половине дуги ST: ∠SRT = 54:2 = 27° Тогда угол ∠S = ∠RST = 180 - 90 - 27 = 63° 3. Так как RT и QS - хорды, то углы, образованные при их пересечении - вертикальные => ∠R + ∠S = ∠Q + ∠T ∠Q = 2x + x + 12 - 2x + 6 = x + 18 ∠S и ∠T - вписанные, опирающиеся на одну и ту же дугу окружности RQ. => ∠S = ∠T x + 12 = 2x - 6 x = 18 2x - 6 = 30° - ∠T x + 18 = 36° - ∠Q Ответ: 36°; 30° 4. ∠С и ∠D - вписанные, опирающиеся на одну и ту же дугу окружности АВ. => ∠С = ∠D 5y - 3 = 2y + 9 3y = 12 y = 4 2y + 9 = 17° - ∠D ∠A и ∠В - вписанные, опирающиеся на одну и ту же дугу окружности CD. => ∠A = ∠В 3x + 9 = 5x - 7 2x = 16 x = 8 5x - 7 = 33° - ∠В Ответ: 17°; 33°

-
Автор:
serrano - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
подобрать материал о труде людей в Арктике 4 класс
-
Предмет:
Окружающий мир -
Автор:
fun sizehozo - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
проверочное слово к слову честный,окрестный,солнце,честность,участники
-
Предмет:
Русский язык -
Автор:
ivyhogan - 5 лет назад
-
Ответов:
5 -
Смотреть
-
-
помогите.
В приведённый ниже предложениях из прочитанного текста пронумерованы все запятые. Выпишите цифры, обозначающие запятые между частями сложного
Я не удивился словам Павла Васильевича. Оставались еще в деревне три-четыре старика. Но последним-то стариком деревни называли только его,(1) Павла Васильевича. Он был из той уходящей породы русских мужиков,(2) которые умели и жить с размахом,(3) и работать всласть,(4) и чудить.
Павел Васильевич умер в тот же день,(5) под вечер,(6) когда садилось солнце.
-
Предмет:
Русский язык -
Автор:
hogan - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
83-49-х=63:9+21, 83-49-х=28
-
Предмет:
Математика -
Автор:
kaylyn - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
