Задать вопрос Регистрация
Помочь другим

  • Найти частное решение диф. уравнения, удовлетворяющее данным начальным условиям y"-6y'+25y=(32x-12)sin x - 36x cos 3x;         y(0) = 4 ; y'(0) = 0

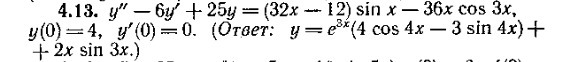
    question img

Ответы 1

  • Крч... либо условия косячные либо хз... но решение на ответ ни разу не походит:y''-6y'+25y=(32x-12)sinx-36xcos(3x)\\\lambda^2-6\lambda+25=0\\\lambda_{1,2}=3^+_-4i\\Y=e^{3x}(C_1cos4x+C_2sin4x)\\\hat{y}=\hat{y}_1+\hat{y}_2\\\hat{y}_1=(Ax+B)cosx+(Cx+D)sinx\\\hat{y}_2=(Ex+F)cos3x+(Gx+H)sin3x\\Тут я тормозну... ибо я на бумаге я замучался их высчитывать... поэтому сразу пропишу готовые значения:\hat{y}_1=(\frac{16}{51}x-\frac{18}{289})cosx+(\frac{64}{51}x-\frac{376}{2601})sinx\\\\\hat{y}_2=(-\frac{144}{145}x-\frac{6858}{21025})cos3x+(\frac{162}{145}x+\frac{8694}{21025})sin3xy=Y+\hat{y}=e^{3x}(C_1cos4x+C_2sin4x)+(\frac{16}{51}x-\frac{18}{289})cosx+\\\\+(\frac{64}{51}x-\frac{376}{2601})sinx+(-\frac{144}{145}x-\frac{6858}{21025})cos3x+(\frac{162}{145}x+\frac{8694}{21025})sin3xА теперь гвоздь программы: константы...C_1=-\frac{371372413}{109372050}\ ;C_2=\frac{26665312}{6076225}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years