Задать вопрос Регистрация
Помочь другим

  • Как это доказывается через индуктивный метод?

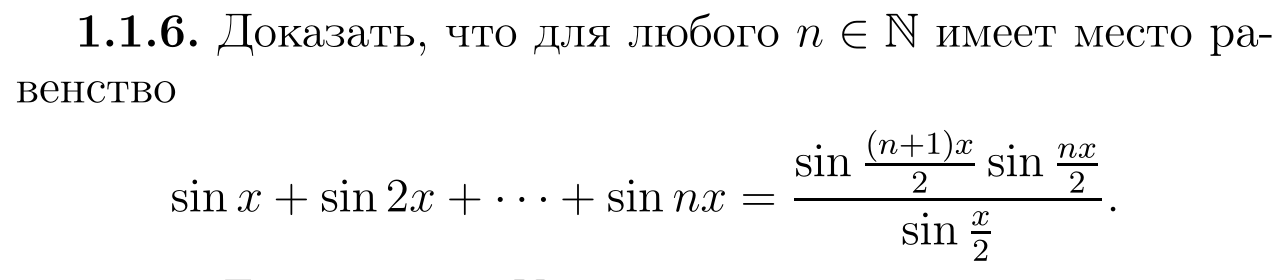
    question img

Ответы 1

  • База индукциипри n=1 тождество верно sin x=\frac{sin \frac{(1+1)x}{2}*sin \frac{1*x}{2}}{sin \frac{x}{2}}Гипотеза индукцииПусть тождество верно при натуральном n=kИндукционный переход Докажем что тогда тождество верно и при n=k+1sin x+sin 2x+...sin kx+sin(k+1)x= используем гипотезу индукции =\frac{sin\frac{(k+1)x}{2}*sin \frac{kx}{2}}{sin \frac{x}{2}}+sin(k+1)x=\frac{sin\frac{(k+1)x}{2}*sin \frac{kx}{2}+sin(k+1)xsin\frac{x}{2}}{sin \frac{x}{2}}=использовали формулу синуса двойного угла и вынесли общий множитель за скобки\frac{\frac{sin(k+1)x}{2}}{sin \frac{x}{2}}*(sin \frac{kx}{2}+2cos \frac{(k+1)x}{2}sin \frac{x}{2})=используем формулу умножения синуса на косинус\frac{\frac{sin(k+1)x}{2}}{sin \frac{x}{2}}*(sin \frac{kx}{2}+sin (\frac{x}{2}- \frac{(k+1)x}{2})+sin (\frac{x}{2}+\frac{(k+1)x}{2}))=обычные преобразования дробей\frac{\frac{sin(k+1)x}{2}}{sin \frac{x}{2}}*(sin \frac{kx}{2}+sin (\frac{-kx}{2})+\sin \frac{(k+2)x}{2})=используем нечетность синуса\frac{\frac{sin(k+1)x}{2}}{sin \frac{x}{2}}*(sin \frac{kx}{2}-sin (\frac{kx}{2})+\sin \frac{(k+2)x}{2})=получаем нужное равенство для n=k+1\frac{\frac{sin(k+1)x}{2}}{sin \frac{x}{2}}*(\sin \frac{(k+2)x}{2})=По приниципу математической индукции тождество верно для любого натурального значения числа n

    • Автор:

      dante18
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years