Задать вопрос Регистрация
Помочь другим

  • помогите решить ! у меня получается дискримант меньше нуля

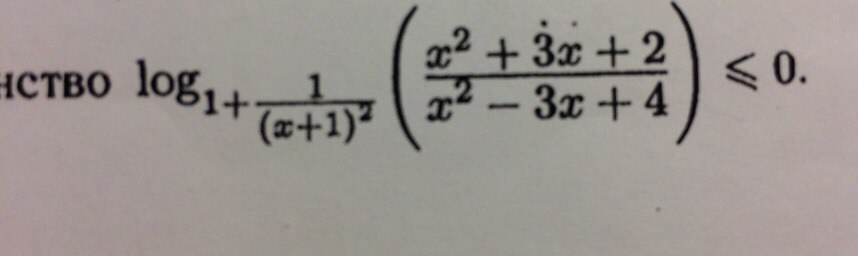
    question img

Ответы 1

  • Основание логарифма больше 1, значит, он возрастающий.Получаем неравенство:0\ \textless \ \frac{x^2+3x+2}{x^2-3x+4} \leq 1 Числитель x^2+3x+2 = (x+1)(x+2)Знаменатель x^2-3x+4 > 0 при любом x. (Дискриминант D < 0)Решением неравенства \frac{x^2+3x+2}{x^2-3x+4} \ \textgreater \ 0 будетx ∈ (-oo; -2) U (-1;+oo)Решаем неравенство\frac{x^2+3x+2}{x^2-3x+4} \leq 1\frac{x^2+3x+2}{x^2-3x+4} -1 \leq 0\frac{x^2+3x+2-x^2+3x-4}{x^2-3x+4} \leq 0\frac{6x-2}{x^2-3x+4} \leq 0Так как x^2-3x+4 > 0 при любом x, то6x - 2 ≤ 0x ≤ 1/3Ответ: x ∈ (-oo; -2) U (-1; 1/3]

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years