-
Найдите производную (подробное решение): ((2x-1)^2)*sqrt(1-2x)
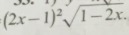
-
Предмет:
Математика -
Автор:
thelma - 6 лет назад
-
Ответы 1
-
=
=
-
Автор:
adelaidag380 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Какой звук русского языка не встречается перед глухими согласными звуками,но встречается после них?
(А) [ж]
(Б) [б]
(В) [в]
(Г) [г]
(Д) [д]
Помогите пожалуйста ,очень нужно!Заранее спасибо!-
Предмет:
Русский язык -
Автор:
finley34 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Составить осложненные предложения со словами:
Диалог
Реплика
Товарищ
Ананас
Драматург
Вообще
Фантазия
Адрес
Чуть-чуть
Рисунок
Земляника
Барьер-
Предмет:
Русский язык -
Автор:
bird - 6 лет назад
-
Ответов:
4 -
Смотреть
-
- Как называется объект в базе которого корабль попал в шторм 42 градуса южной широты и 173 западной долготы.
- (-2a^2b)^2(-a^2b^3)^3
How much to ban the user?
1 hour
1 day
100 years
