-
Помогите решить. Вычислить приближенно определенный интеграл с точностью 0,001
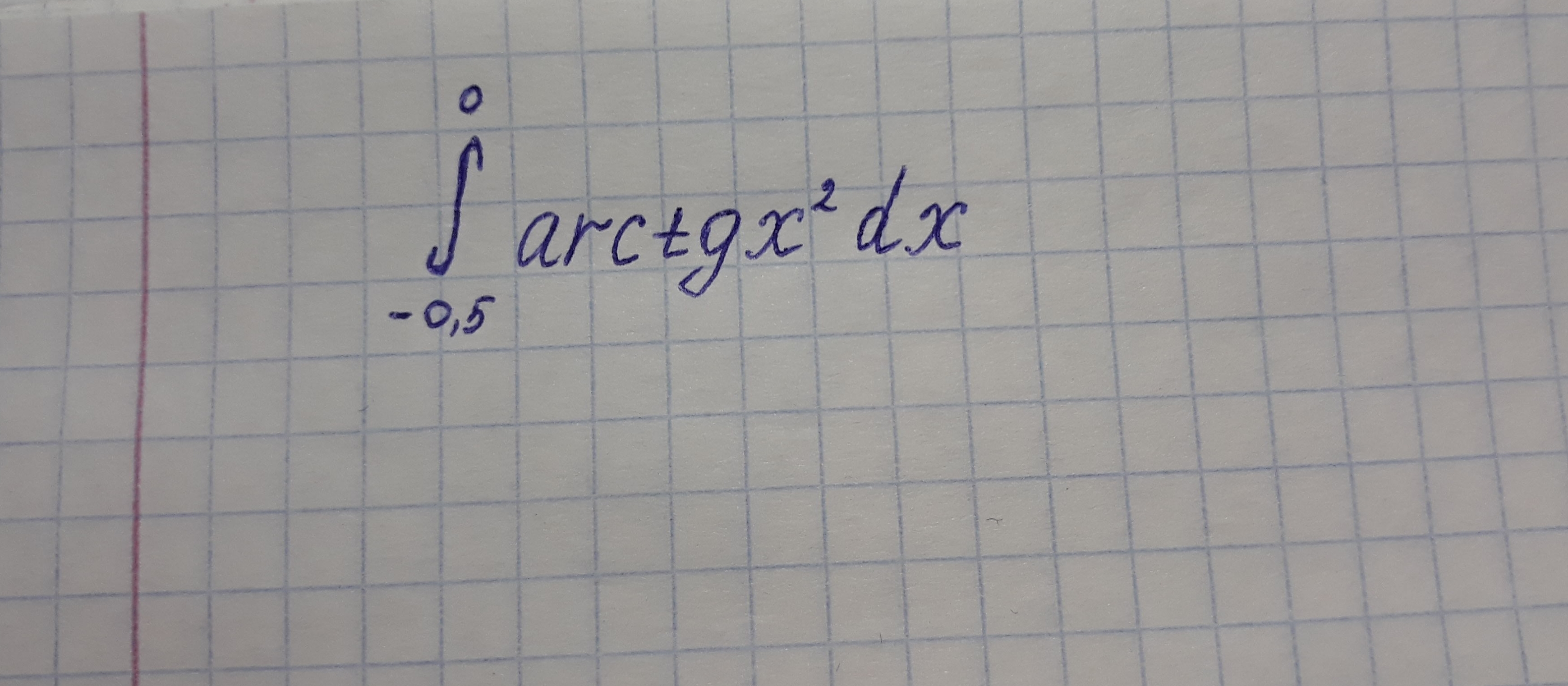
-
Предмет:
Математика -
Автор:
pintoulxx - 5 лет назад
-
Ответы 1
-
Рассмотрим функцию
Оценим её максимальное значение на отрезке
. На этом отрезке она дифференцируема,
Оцениваем второй интеграл:
Его значение меньше допустимой погрешности, его можно отбросить.
Ответ. 0,041
-
Автор:
weiner - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Описание Дмитрия Нагиева, как телеведущего.
-
Предмет:
Русский язык -
Автор:
benjamínfkgv - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Начерти 2 таких квадрата,чтобы периметр первого был равен 8 см, а периметр второго был бы в
3 раза больше математика 1 часть 3 класс учебник -
Помогите там надо списать только разделительные ь и ъ
-
Предмет:
Русский язык -
Автор:
tristan15 - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
помогите решить!
Найти приближённое значение приращения функции:
y=3x² +5x -1 x0=5. ∆x=0,01-
Предмет:
Математика -
Автор:
cannondillon - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
