-
Помогите Найти неопределенный интеграл, с полным решением пожалуйста
1) ∫3/x^2 -1-4/(x^2+9) dx
2) ∫sin(2-3x)dx
3) ∫dx/(arc sin^3*x√(1-x^2 ))
4) ∫(4x-1)/((x-1)(x+2)) dx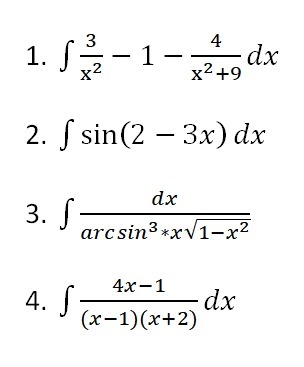
-
Предмет:
Математика -
Автор:
loganzg5j - 5 лет назад
-
Ответы 3
-
Спасибо большое
-
Автор:
ruforodgers - 5 лет назад
-
0
-
-
Большое пожалуйста!
-
Автор:
currydelgado - 5 лет назад
-
0
-
-
1) Совсем просто, по табличным интеграламInt = -3/x - x + 4/3*arctg(x/3) + C2) Тоже просто, по формуле с коэффициентом Int f(ax) dx = 1/a*F(ax) + CInt = 1/(-3)*(-cos(2 - 3x)) + C = 1/3*cos(2 - 3x) + C3) Замена arcsin x = t; dt = dx/√(1 - x^2)Int dt/ t^3 = Int (t^(-3)) dt = t^(-2)/(-2) + C = -1/2*(arcsin x)^(-2) + C4) По методу неопределенных коэффициентов
Коэффициенты при одинаковых степенях должны быть равны{ A + B = 4{ 2A - B = -1Отсюда A = 1; B = 3
-
Автор:
kendall10 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
У какого животного больше всего хромосом ?
-
Предмет:
Геометрия -
Автор:
geniemcgee - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- Почему при смешивании растворов хлорида алюминия и карбоната калия не образуется карбонат алюминия?
-
this plant is rare met in france
-
Предмет:
Английский язык -
Автор:
big nastyshyo - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
заполните таблицу , сравнив параллели и меридиан
-
Предмет:
География -
Автор:
micaelamooney - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
