-
Помогите пожалуйста решить!
дифференцированное уравнение кто умеет и может!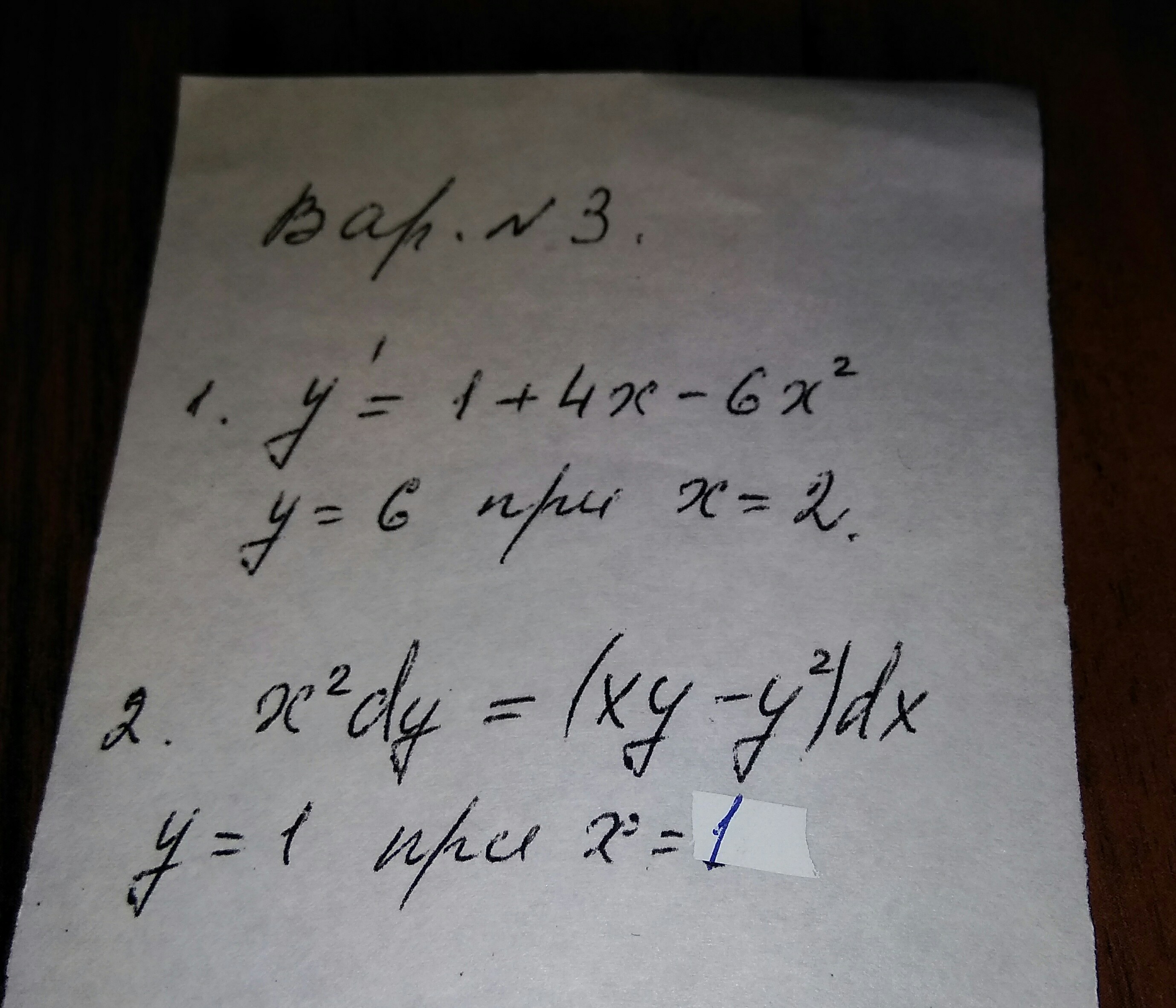
-
Предмет:
Математика -
Автор:
romualdouwu1 - 5 лет назад
-
Ответы 1
-
1. Интегрируя левую и правую части уравнения, получим
Получили это общее решение ДУ. Осталось найти частное решение, подставив начальные условия.
частное решение2. Переписав данное ДУ в следующем виде
. И этот вид ДУ является однородным(выполняется условие однородности).Пусть
тогда по правилу дифференцирования произведения двух функций :
И это последнее уравнение является ДУ с разделяющимися переменными
тогда, осуществив замену
, получим
Подставляя начальные условия, получим частное решение:
- частное решение.
-
Автор:
oren - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
1 вариант надо! помогите!!
очень много баллов даю!!!!-
Предмет:
Геометрия -
Автор:
cristianwells - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
короткое описание Платова в рассказе Левша
-
Предмет:
Литература -
Автор:
sweetie-piekkcn - 5 лет назад
-
Ответов:
6 -
Смотреть
-
-
7 класс медвежья семья
-
Предмет:
Русский язык -
Автор:
jasperrowe - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
помогите, пожалуйста!
никто не знает, откуда эти задания? хочу прорешать весь учебник.
How much to ban the user?
1 hour
1 day
100 years
