Задать вопрос Регистрация
Помочь другим

  • Пример 4. Исследовать на сходимость следующие числовые ряды:

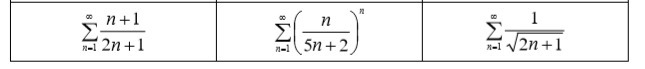
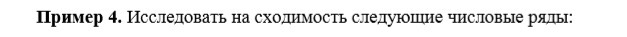
    question img
    question img

Ответы 1

  • 1. Здесь можно сразу проверить на необходимый признак сходимости ряда\displaystyle \lim_{n \to \infty} \frac{n+1}{2n+1}= \frac{1}{2} e 0Условие необх. сходимости ряда не выполняется, следовательно, данный ряд расходится.2. По признаку Коши   \displaystyle \lim_{n \to \infty} \sqrt[n]{\bigg( \frac{n}{5n+2}\bigg)^n } =\lim_{n \to \infty} \frac{n}{5n+2} = \frac{1}{5} \ \textless \ 1Ряд является сходящимся.3. \displaystyle \sum^\infty_{n=1} \frac{1}{\sqrt{2n+1}} \dfrac{1}{\sqrt{2n+1}} \leq \dfrac{1}{ \sqrt{2} n^{1/2}} Поскольку \displaystyle \sum^\infty_{n=1}\dfrac{1}{n^{1/2}} является сходящимся, то и исходный ряд тоже сходится по первому признаку сравнения

    • Автор:

      jamie34
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years