-
Пожалуйста, помогите с решением уравнения и системы
даю 45 баллов!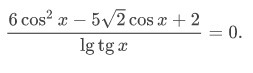
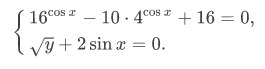
-
Предмет:
Математика -
Автор:
dollqsgy - 5 лет назад
-
Ответы 2
-
Написала, ответ в закреплении

-
Автор:
rafael435 - 5 лет назад
-
0
-
-
1{16^cosx-10*4^cosx+16=0 (1){√y+2sinx=0 (2)1)4^cosx=tt²-10t+16=0T1+t2=10 U t1*t2=16t1=8⇒2^2cosx=3⇒cosx=1,5>1 нет решенияt2=2⇒2^2cosx=1⇒cosx=1/2⇒x=-π/3 U cosx=π/3sinx=√(1-cos²x)=+-√(1-1/4)=+-√3/22)√y+2*(-√3/2)=0⇒√y=√3⇒y=3√y+2*√3/2=0⇒√y=-√3 нет решенияОтвет (-π/3+2πk,k∈z;3)2ОДЗ lgtgx≠0⇒tgx≠1⇒x≠π/4+πk,k∈zcosx=t6t²-5√2t+2=0D=50-48=2t1=(5√2-√2)/12=√2/3⇒cosx=√2/3⇒x=+-arccos√2/3+2πk,k∈zt2=(5√2+√2)/12=√2/2⇒cosx=√2/2x=-π/4+2πk,k∈z U x=π/4+2πk,k∈z не удов ОДЗОтвет x={-π/4+2πk,k∈z ;+-arccos√2/3+2πk,k∈z}

-
Автор:
william629 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
1). Переведите предложения на английский язык, употребляя глаголы в Present Simple
1. Я работаю. 2. Мы работаем. 3. Они не работают. 4. Вы работаете? – Нет. Он учится. 6. Мой брат не учится. Он работает. 7. Ты носишь очки? 8.Вы помогаете людям? 9. Он любит читать сказки? 10. Она любит играть на скрипке. 11. Моя сестра не читает книг. 12. Наша бабушка любит спать на диване.-
Предмет:
Английский язык -
Автор:
cujosantos - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
4sin^3xcosx-4cos^3xsinx=1
HELP-
Предмет:
Алгебра -
Автор:
aguilarzwra - 5 лет назад
-
Ответов:
2 -
Смотреть
-
- Определите количество гидроксида натрия в образце массой 10г
- Решите дифференциальное уравнение второго порядка. Подробно, с решением: y`` + 9y = 15*sin(2*x). Школа, 11 класс, простая задача.
How much to ban the user?
1 hour
1 day
100 years
