-
Найдите c, M(x), D(x), F(x), P(5 ной величины X имеет вид:
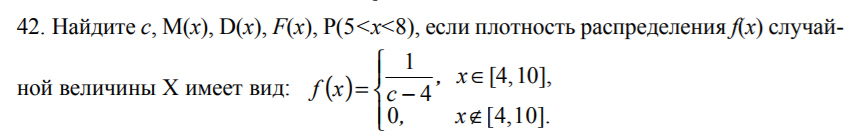
-
Предмет:
Математика -
Автор:
gary - 5 лет назад
-
Ответы 1
-
Параметр с из условия: \displaystyle \int\limits^{b}_a f(x)dx=1\displaystyle \int\limits^{10}_4 \frac{dx}{c-4}= \frac{x}{c-4}\bigg|^{10}_4= \frac{10-4}{c-4} = \frac{6}{c-4}=1;~~~~~\Rightarrow~~~~~ \boxed{c=10}Математическое ожидание: M(x)=\displaystyle \int\limits^b_a {xf(x)} \, dx = \int\limits^{10}_4 \frac{xdx}{6} = \frac{x^2}{12}\bigg|^{10}_4 =7Дисперсия: \displaystyle D(x)=(M(x))^2-M(x)^2=3Функция распределения: \displaystyle \begin{cases} & \text{ } 0,~~~~~~~~~~~~~x \leq 4 \\ & \text{ } \dfrac{x}{6}- \dfrac{2}{3},~~~~~~ 4\ \textless \ x \leq 10 \\ & \text{ } 1,~~~~~~~~~~~~~x\ \textgreater \ 10 \end{cases}Вероятность того, что случайная величина х примет значения из интервала (5;8) равна: P\{5\ \textless \ x\ \textless \ 8\}=F(8)-F(5)= \dfrac{2}{3}- \dfrac{1}{6} = \dfrac{1}{2}
-
Автор:
juanyohz - 2 года назад
-
11
-
-
Добавить свой ответ
Еще вопросы
-
возраст рябины 100 лет что составляет 2/3 от продолжительности жизни березы Какова продолжительность жизни березы
-
Предмет:
Математика -
Автор:
keeshacalderon - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Замените выражение тождественно равным , используя правило раскрытия скобок:(2х+у)-(х+у)
-
Предмет:
Математика -
Автор:
kyliemn4u - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
прочитай стихотворение Р.Сефа.Определи склонение имён существительных распредели их по трём колонкам:1-е,2-е,3-е склонение.Выдели окончания. На свете всё На всё похоже: Зм_я_ На рем_шок Из кож__,Луна __ На круглый гла_ Огромный;Журавль _ на тощий Кран пол__ёмный; Ко_ пол_сатый_ На пижаму;Я__на тебя, А ты __на маму.
-
Предмет:
Русский язык -
Автор:
rafaelbishop - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
Два автомата за 3 минуты закрывают 567 банок причем первый автомат в минуту закрывает на 9 банок больше чем второй.
1)Сколько банок за минуту закрывает каждый автомат?
2)За сколько минут оба автомата закроют 3780 банок работая с той же производительностью?-
Предмет:
Математика -
Автор:
dummytych - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
